一文理解Attention:从起源到MHA,MQA和GQA。Attention模块是现在几乎所有大模型的核心模块，因此也有很多工作致力于提升注意力计算的性能和效果。主要内容有：关于Attention、从RNN到Attention、Transformer的attention、MHA、MQA、GQA、KV Cache等。

一文理解Attention:从起源到MHA,MQA和GQA

Attention模块是现在几乎所有大模型的核心模块，因此也有很多工作致力于提升注意力计算的性能和效果。其中MHA（Multi-Head Attention）、MQA（Multi-Query Attention）和GQA（Grouped-Query Attention）这一路线的思路和做法被很多主流模型所采用，因此简单地梳理一些这几个变体的思路和做法，以及会涉及到的KV Cache相关内容。思路比较直白，但也有一些细节和原理值得思考。

当然针对Attention优化，也有很多其他优秀的方案和思路，如线性注意力、FlashAttention和Sliding Window Attention等，这些在后续再开篇梳理。

1.关于Attention：从RNN到Attention

了解一个概念的诞生和演进，有助于我们更深入去理解它。我们先简单回顾下attention从起源到最初的实现。

（熟悉attention的朋友可以跳过这一节）

1.1.从RNN说起

Memory is attention through time. ~ Alex Graves 2020

注意力机制最初起源是为了解决序列问题。回想在还没有Transformer的上一世代，使用RNN的Seq2Seq是这样的

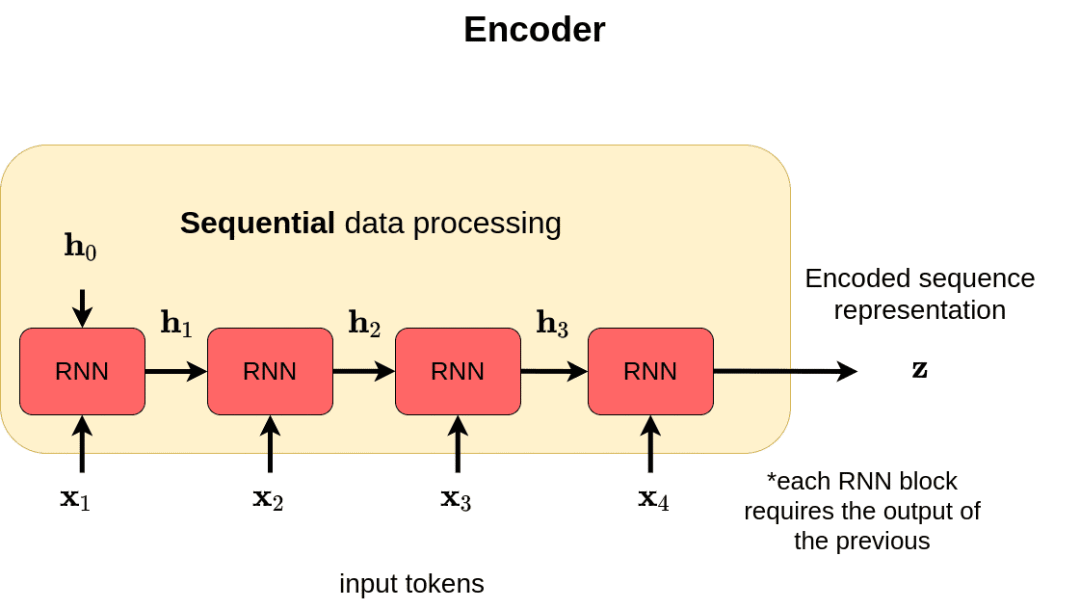
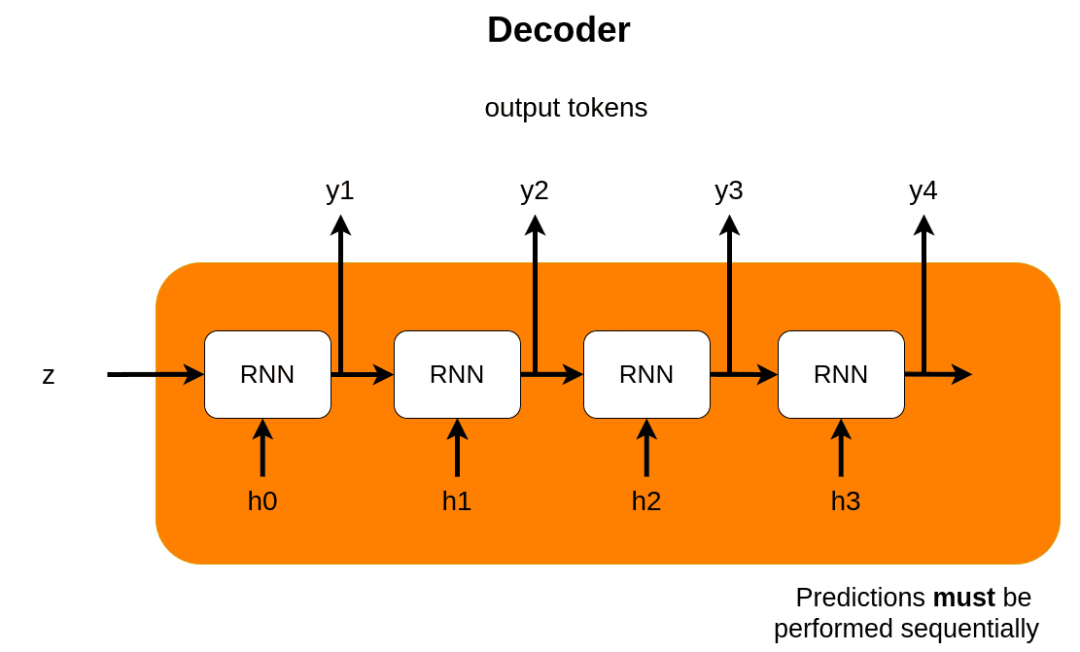
每个RNN cell接收两个输入, 输出一个hidden state。比如在㗲译任务中, RNN encoder把所有输入迭代地编码成context向量 $z$ ，然后由RNN decoder基于 $z$ 迭代地解码。一般来说，这里 decoder的第一个输入是一个特殊token, 如[start], 表示解码开始。

这样会有一个问题， $z$ 能编码的长度显然有限，而且由于模型结构问题，会更加关注靠近尾部的输入。这样如果关键信息出现在开头，就容易被忽略。

并且时间步骤上的传播由于有多次迭代相乘，梯度很容易就过小，导致梯度消失问题。

当然我们有LSMT和GRU等变体来增强长距离记忆的能力，也缓解了梯度问题，但这些方案还是没有产生质变的能力。

回到问题的核心，我们想要 $z$ 能够编码所有前面的内容，但是显然， $z$ 的生成方式天然会让它更容易注意到靠后的内容, 而容易忽路靠前的输入。

一个直觉的想法就是, 我们需要想个办法跳过 $z$, 和前面的每个输入建立直接的联系。我们希望模型能够有机会学习到去”注意”关键的输入，不管这个输入是在前面还是后面。

实际上神经网络天生就具有”注意力”的天倵。

比如在CNN分类中，如果我们屆出分类层前的heatmap，会是如下图这个样子

可以看到，值比较高的地方是在猫的鼻子胡子嘴巴区域，次之是身上和头上的花纹。直观来说，就是模型主要通过脸部的特征和身上的花纹，来识别出这是一只猫。这就是CNN学习到的注意力，这样的特征是神经网络implicitly学到的。

回归到Seq2Seq，我们怎么来实现注意力，并且让这种implicit的机制变得explicit：单独抽离出来并具备一定可控制性?

回想翻译场景，在RNN中，每一个时间步骤 $i$ 都会产生一个隐向量， $h_{i}$ 向量，我们把这些 $h_{i}$ 保存起来，在最后要生成新的输出的时候，我们让模型回头看一下之前的这每一个 $h_{i}$ ，再决定要生成什么内容。相比原来只利用最后一个hidden state，现在我们可以访问之前所有的中间状态，如果发现前面有关键信息，就可以直接用上了，而不用担心输入太长而被覆盖了。

那么问题又来了，我们怎么知道前面某一个中间状态对于当前的生成来说是否重要？如果我们不知道怎么定义是否重要，那我们就把这个问题交给模型自己解决好了 – 通过网络参数来学习识别某个输入状态是否重要，学习是否要”注意”到它，要给予多少的”注意力”。

具体来说，我们定义在解码第 $i$ 个输出是， decoder当前隐状态 $y_{i-1}$ 和encoder的所有隐状态 $\mathbf{h}$之间的一个score计算

其中

注意力网络通过 $y_{i-1} 和 h_j 来计算一个值 e_{i j}$, 这里的注意力网络可以设计各种操作, 比如对输入进行拼接再通过fc层进行计算等。

这里 $e_{i j}$ 是一个标量，但它还不是一个可用的权重值，还需要通过一个函数，把attention net对各个encoder hidden state的输出值转成一个分布：softmax。

最后通过加权计算，获得最终输入给decoder的隐变量。

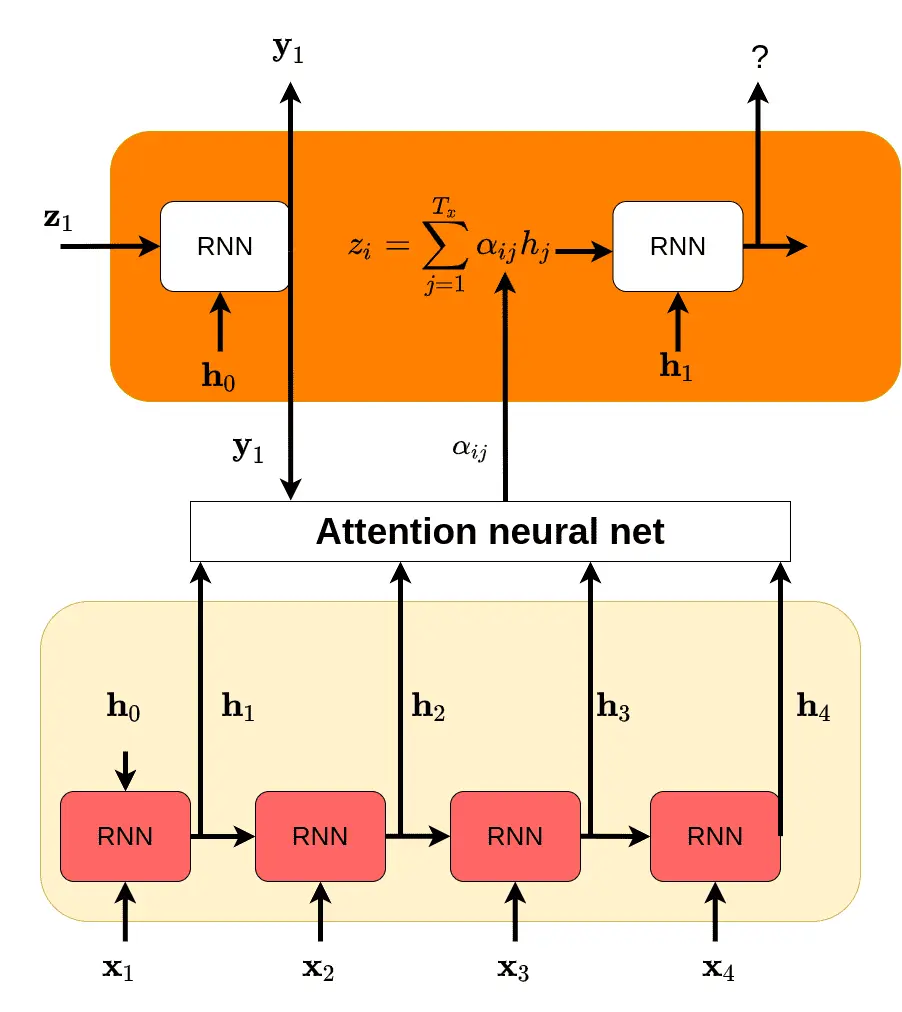
可以看到，这里的attention net的任务就是找到decoder上一个hidden state和encoder hidden state之间的”相关”关系，使得模型能够将更多的注意力放在对应的输入信息上。

实际上，上面这种attention的计算方式并不是唯一的，attention的计算方式有许多种

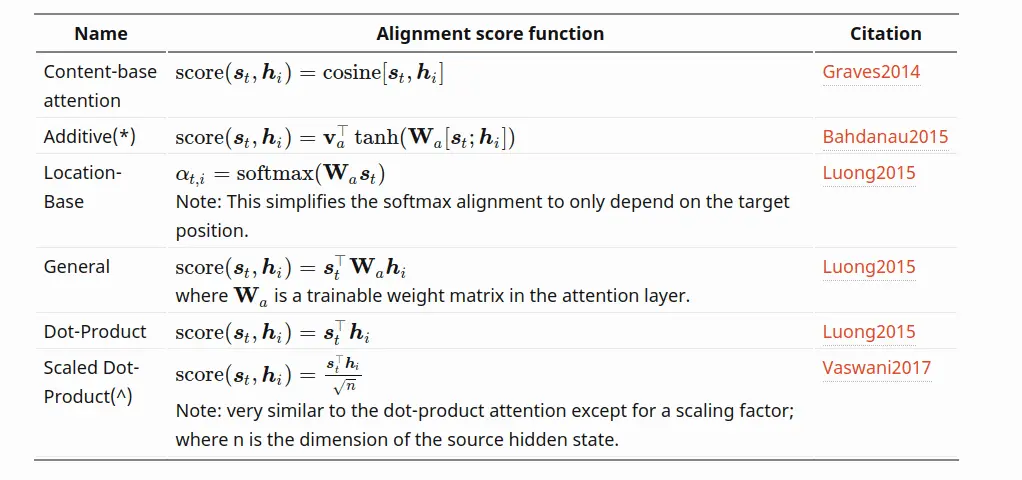
这些attention的一般形式可以写作 $\operatorname{Attention}(s, h)=\operatorname{Score}(s, h) \cdot h$ 。这里的 $s$ 就是 decoder的hidden state（也就是前文的 $y$ ）， $h$ 就是encoder的hidden state。

（当然从结果上看，是scaled dot-product attention经受住了历史的考验，成为了主流。）

1.2.Transformer的attention

从RNN attention到transformer attention，所做的事情就如论文题目所说：《Attention Is All You Need》，彻底地弃RNN的在time step上的迭代计算，完全拥抱attention机制，只用最简单粗暴的方式同步计算出每个输入的hidden state，其他的就交给attention来解决。

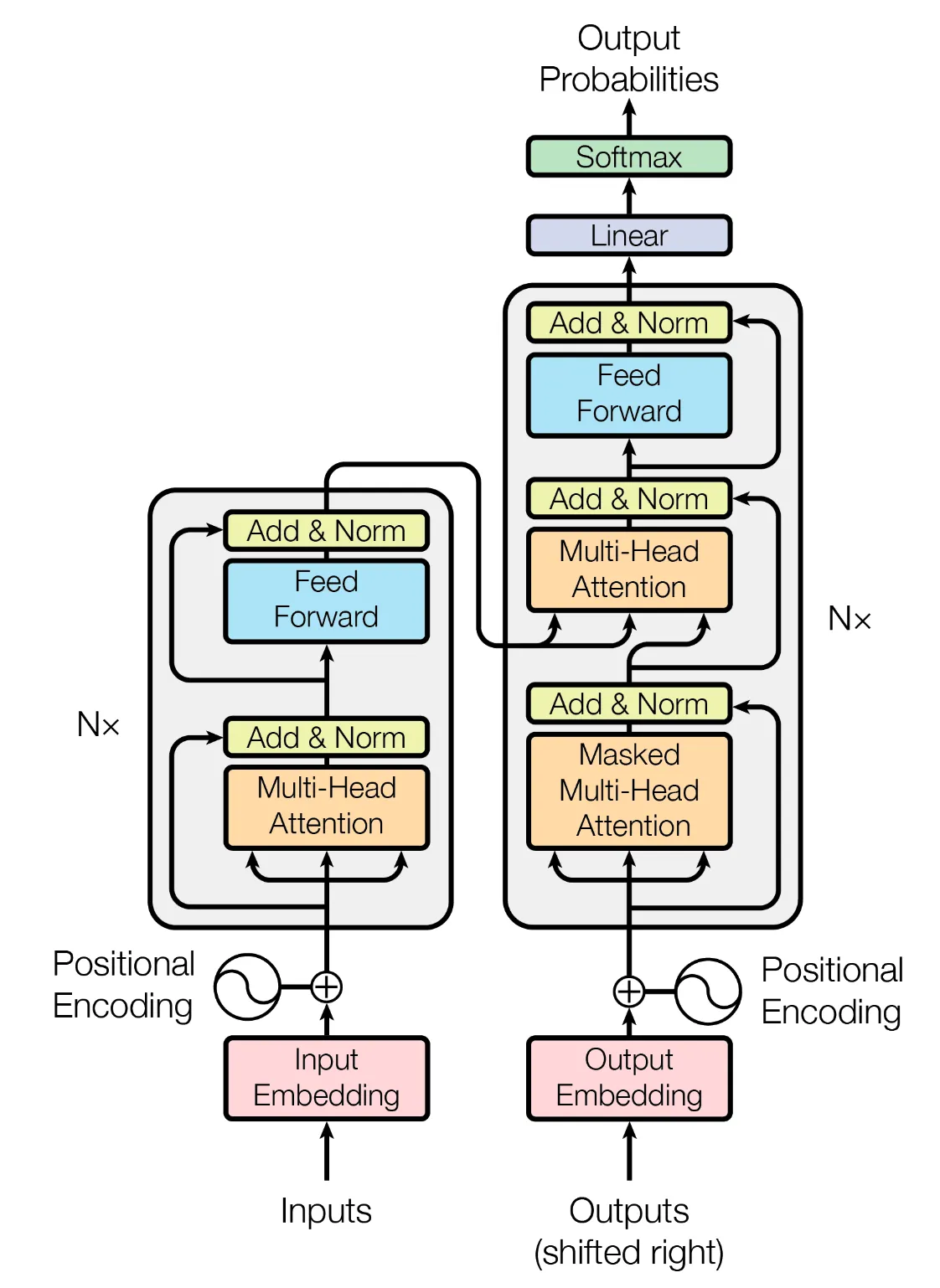
这里还是保留有encoder和decoder的结构, encoder中的attention都是self-attention, decoder 则除了 self-attention还有cross-attention。

transformer结构下，attention的一般形式可以写作 $\operatorname{Attention}(Q, K, V)=\operatorname{Score}(Q, K) V$ ，这里有 $Q=W_{Q} Y, K=W_{K} X, V=W_{V} X$ 。对于cross-attention, $X$ 是encoder的 hidden states, $Y$ 是decoder的hidden states，而对于self-attention，则有 $X=Y$ 。

具体到我们熟悉的scaled dot-product attention，使用softmax计算，有

到这里，终于见到我们熟悉的attention计算。

用一张很直观的图来展示整个计算

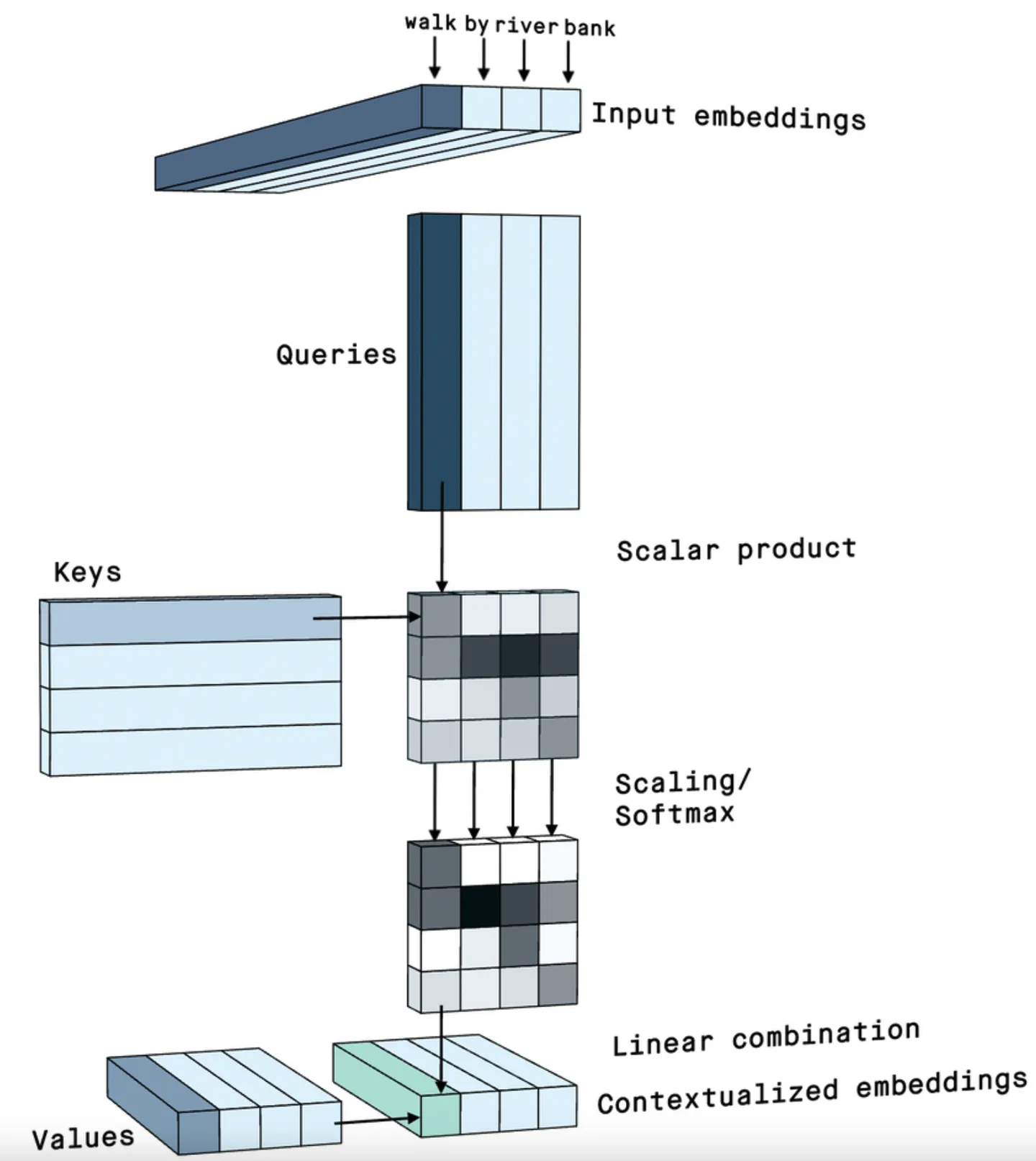
这里的「query」, 「key」 和「value」 的名称也暗示了整个attention计算的思路。

类比到一个数据库查询+预测的例子。

假设我们现在有一个”“文章-阅读量”数据库，记录了每篇文章在发布30天内的阅读量。每篇文章就是一个key, 对应的阅读量就是value。

我们现在有一篇将要发布的文章, 想要预测这篇文章在30天内的阅读量, 那我们就把这篇新的文章, 作为query, 去和数据库里的文章 (key) 做一个相关性计算, 取最相关的5篇文章。

假设top5篇文章的相关性分别是 $[8,4,4,2,2]$, 对应阅读量是 $[5 \mathrm{w}, 2 \mathrm{w}, 8 \mathrm{w}, 3 \mathrm{w}, 6 \mathrm{w}]$ 。

那我们把相关性得分归一化成和为1的概率值 $[0.4,0.2,0.2,0.1,0.1]$ ，那我们就可以预测新文章 30 天内的阅读量是 $0.4 \times 5+0.2 \times 2+0.2 \times 8+0.1 \times 3+0.1 \times 6=4.9 \mathrm{w}$ 。

这个例子中，我们计算相关性就相当于transformer attention中的 $Q K^{T}$ ，归一化就是softmax，然后通过加权求和取得最后的阅读量特征向量。

对于self-attention, $Q 、 K 、 V$ 都来自输入 $X$, sequence自己计算自己每个token的之间的相关性。而对于cross-attention, decoder中的输出sequence就是上面这个例子中的”将要发布的文章”，通过把这篇新的文章和数据库中的文章做相关计算，我们得到了新的预测结果。

对于self-attention，由于 $Q 、 K 、 V$ 都来自输入 $X$ ，在计算 $Q K^{T}$ 时，模型很容易关注到自身的位置上, 也就是 $Q K^{T}$ 对角线上的激活值会明显比较大。这样的情况其实不是很好, 因为这会削弱模型关注其他高价值位置的能力，也就限制模型的理解和表达能力。后面讲的MHA对这个问题会有一些缓解作用。

顺着这样的思路梳理下来, 会发现attention的大思路还是很好理解的。而计算上, 怎么去获得更好的效果, 就是接下来要分析的几个内容, MHA, MQA和GQA所关注的。

代码上, 实现也很容易, 直接看pytorch forcasting的代码

class ScaledDotProductAttention(nn.Module):
    def __init__(self, dropout: float = None, scale: bool = True):
        super(ScaledDotProductAttention, self).__init__()
        if dropout is not None:
            self.dropout = nn.Dropout(p=dropout)
        else:
            self.dropout = dropout
        self.softmax = nn.Softmax(dim=2)
        self.scale = scale

def forward(self, q, k, v, mask=None):
        attn = torch.bmm(q, k.permute(0, 2, 1))  # query-key overlap

        if self.scale:
            dimension = torch.as_tensor(k.size(-1), dtype=attn.dtype, device=attn.device).sqrt()
            attn = attn / dimension

        if mask is not None:
            attn = attn.masked_fill(mask, -1e9)
        attn = self.softmax(attn)

        if self.dropout is not None:
            attn = self.dropout(attn)
        output = torch.bmm(attn, v)
        return output, attn

1.3.关于scaling

BTW, 为什么计算中 $Q K^{T}$ 之后还要除以 $\sqrt{d}$

简单来说，就是需要压缩softmax输入值，以免输入值过大，进入了softmax的饱和区，导致梯度值太小而难以训练。 苏剑林的博客中也有详细分析，并提到如果不对attention值进行scaling，也可以通过在参数初始化是将方羞除以一个 $\sqrt{d}$, 同样可以起到预防softmax饱和的效果。类似地, 通过normalization也可以做到类似的效果。不过实现上在attention里做scaling还是比较稳定高效的。

2.MHA

只要理解了attention计算的细节，MHA（multi-head attention）其实就很好明白。

MHA在2017年就随着 《Attention Is All You Need》一起提出，主要干的就是一个事：把原来一个 attention计算，拆成多个小份的attention，并行计算，分别得出结果，最后再合回原来的维度。

MultiHeadAttention $(Q, K, V)=$ Concat $\left(\right.$ head $_1, \ldots$, head $\left.h\right)$

假设原来模型的hidden size是 $d$ ，在MHA中，会把投影后的 $Q 、 K 、 V$ 在hidden state的维度上切成 $h e a d_{n u m}$ 份，每个头的维度是 $d_{\text {head }}$ 。这 head $d_{n u m}$ 组小 $Q 、 K 、 V$ 分别独立地进行 attention计算，之后把得到的 head $d_{n u m}$ 份维度 $d_{\text {head }}$ 的输出concat起来。

直接看这个amazing的图，很直观

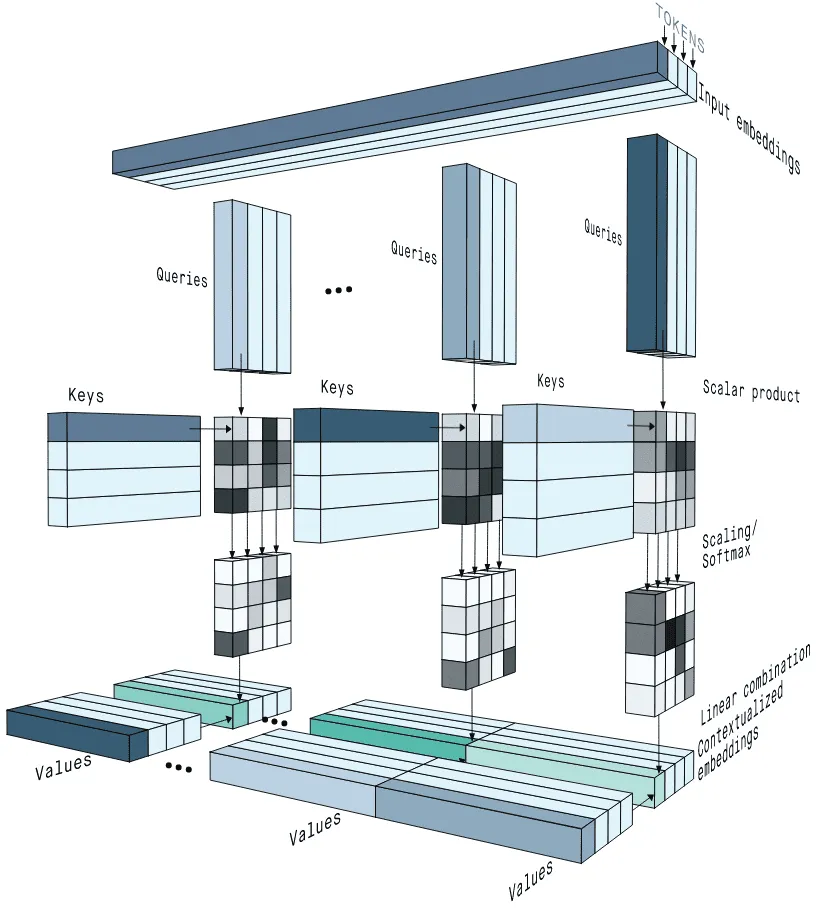
操作是这么个操作，多头注意力相比单头有什么好处呢?

《Attention Is All You Need》文章中给出的说法是

Multi-head attention allows the model to jointly attend to information from different representation subspaces at different positions.

我们希望多个头能够在训绕中学会注意到不同的内容。例如在翻译任务里, 一些attention head可以关注语法特征, 另一些attention head可以关注单词特性。这样模型就可以从不同角度来分析和理解输入信息，获得更好的效果了。

这有点类似CNN中，不同的卷积核来学习不同的信息。比如一个 $3 \times 3 \times 128$ 的卷积，有 128 个 $3 \times 3$ 参数组，假设我们的输入是一个灰度图，其中一组 $3 \times 3$ 的参数是这样的

那么这是一个检测纵向边界的卷积, 而另外一组参数长这样

这是一个检测横向边界的卷积。

这 128 组 $3 \times 3$ 就是128个不同特征的检测器，就同MHA中多个头一样，从不同的子空间学到不同的内容，最后再放到一起融合使用。 知乎上这篇文章里对此做了一些实验和分析。简单来说就是 (1) 每个头确实学到东西有所不同,但大部分头之间的差异设有我们想的那么大（比如一个学句法，一个学词义这样明显的区分）（2）多个头的情况下，确实有少部分头可以比较好地捕捉到各种文本信息，而不会过分关注自身位置，一定程度绶蛘了上文提到的计算 $Q K^{T}$ 之后对角线元素过大的问题。

我们可以把MHA的多个attention计算视为多个独立的小模型，那么最终整体的attention计算相当于把来自多个小模型的结果进行了融合，这样效果比较好也是比较符合直觉的。

另外还有一个问题是，使用几个头比较好呢?

实际上这个问题比较难有确定性的答案，首先可以确定的是头的数量不是越多约好（毕竟头的数量多了，各个子空间小了，子空间能表达的内容就少了）, 具体多少要视模型规模, 任务而定。另外《Are Sixteen Heads Really Better than One?》 中也指出MHA并不总是优于单头的情况。

目前可以看到的趋势是，模型越大（也就是hidden size越大），头数的增离越能带来平均效果上的收益（或者说允许注意力头增大而不影响子空间的学习能力）。目前LLM主流的头数视乎模型结构和规模, 大致有12、16、24、48、96这样一些主流设置。这里面又有比较多的方向和工作, 在此暂时不展开, 挖个坑, 以后专门开一篇讲。

最后看一下The Annotated Transformer中的MHA代码实现

def attention(query, key, value, mask=None, dropout=None):
    "Compute 'Scaled Dot Product Attention'"
    d_k = query.size(-1)
    scores = torch.matmul(query, key.transpose(-2, -1)) \
             / math.sqrt(d_k)
    if mask is not None:
        scores = scores.masked_fill(mask == 0, -1e9)
    p_attn = F.softmax(scores, dim = -1)
    if dropout is not None:
        p_attn = dropout(p_attn)
    return torch.matmul(p_attn, value), p_attn

class MultiHeadedAttention(nn.Module):
    def __init__(self, h, d_model, dropout=0.1):
        '''
        h: head number
        '''
        super(MultiHeadedAttention, self).__init__()
        assert d_model % h == 0
        # We assume d_v always equals d
        self.d = d_model // h
        self.h = h
        self.linears = clones(nn.Linear(d_model, d_model), 4)
        self.attn = None
        self.dropout = nn.Dropout(p=dropout)
        
    def forward(self, query, key, value, mask=None):
        if mask is not None:
            # Same mask applied to all h heads.
            mask = mask.unsqueeze(1)
        nbatches = query.size(0)
        
        # 1) Do all the linear projections in batch from d_model => h x d 
        query, key, value = \
            [l(x).view(nbatches, -1, self.h, self.d).transpose(1, 2)
             for l, x in zip(self.linears, (query, key, value))]
        
        # 2) Apply attention on all the projected vectors in batch. 
        x, self.attn = attention(query, key, value, mask=mask, 
                                 dropout=self.dropout)
        
        # 3) "Concat" using a view and apply a final linear. 
        x = x.transpose(1, 2).contiguous() \
             .view(nbatches, -1, self.h * self.d)
        return self.linears[-1](x)

(transformers中的写法就更为成熟一点，不过里面兼容了比较多的功能，代码太长就不放上来了)

3.解码中的KV Cache

在讲MQA和GQA之前，还需要了解一点背景，那就是解码的计算问题，以及KV Cache的方案。

无论是encoder-decoder结构, 还是现在我们最接近AGI的decoder-only的LLM, 解码生成时都是自回归auto-regressive的方式。

也就是，解码的时候，先根据当前输入 $input_{i-1}$，生成下一个 $token_i$；

然后把新生成的 $token_{i}$ 拼接在 $input_{i-1}$ 后面，获得新的输入 $input_{i}$；

再用 $input_{i}$ 生成 $token_{i+1}$ ，依此迭代，直到生成结束。

比如我们输入”窗前明月光下一句是”，那么模型每次生成一个token，输入输出会是这样（方便起见, 默认每个token都是一个字符）

(其中[BOS]和[EOS]分别是起始符号和终止符号)

仔细想一下, 我们在生成”疑”字的时候, 用的是输入序列中”是”字的最后一层hidden state, 通过最后的分类头预测出来的。以此类推, 后面每生成一个字, 使用的都是输入序列中最后一个字的输出。 我们可以注意到，下一个step的输入其实包含了上一个step的内容，而且只在最后面多了一点点 (一个token)。那么下一个step的计算应该也包含了上一个step的计算。

从公式上来看是这样的:

回想一下我们attention的计算

注意对于decoder的时候，由于mask attention的存在，每个输入只能看到自己和前面的内容，而看不到后面的内容

假设我们当前输入的长度是3, 预测第 4 个字, 那每层attention所做的计算有

预测完第 4 个字, 放到输入里, 继续预测第5个字, 每层attention所做的计算有

可以看到，在预测第 5 个字时，只有最后一步引入了新的计算，而 $o_{0}$ 到 $o_{2}$ 的计算和前面是完全重复的。 但是模型在推理的时候可不管这些，无论你是不是只要最后一个字的输出，它都把所有输入计算一遍，给出所有輸出结果。

也就是说中间有很多我们用不到的计算，这样就造成了浪费。

而且隨着生成的结果越来越多，输入的长度也越来越长，上面这个例子里，输入长度就从step0的 10个，每步增长1，直到step5的15个。如果输入的instruction是让模型写作文，那可能就有 800 个 step。这个情况下, step0被算了800次, step1被算了799次…这样浪费的计算资源确实不容慈视。

有没有什么办法可以重复利用上一个step里已经计算过的结果, 减少浪费呢?

答案就是KV Cache，利用一个缓存，把需要重复利用的中间计算结果存下来，减少重复计算。

而 $k$ 和 $v$ 就是我要缓存的对象。

想象一下，在上面的例子中，假设我们一开始的输入就是 3 个字，我们第一次预测就是预测第 4 个字，那么由于一开始没有任何缓存，所有我们每一层还是要老实地计算一遍。然后把 $k 、 v$ 值缓存起来。

则有

kv_cache的下标 $l$ 表示模型层数。

在进行第二次预测，也就是预测第 5 个字的时候，在第 $l$ 层的时候，由于前面我们缓存了每层的 $k$、 $v$ 值，那本层就只需要算新的 $o_{3}$ ，而不用算 $o_{0} 、 o_{1} 、 o_{2}$ 。

因为第 $l$ 层的 $o_{0} 、 o_{1} 、 o_{2}$ 本来会经过FNN层之后进到 $l+1$ 层，再经过新的投影变换，成为 $l+1$ 层的 $k 、 v$ 值，但是 $l+1$ 层的 $k 、 v$ 值我们已经缓存过了！

然后我们把本次新增算出来的 $k 、 v$ 值也存入缓存。

这样就节省了attention和FFN的很多重复计算。

transformers中, 生成的时候传入use_cache=True就会开启KV Cache。

也可以简单看下GPT2中的实现，中文注释的部分就是使用缓存结果和更新缓存结果

Class GPT2Attention(nn.Module):
    ...
    ...
    def forward(
        self,
        hidden_states: Optional[Tuple[torch.FloatTensor]],
        layer_past: Optional[Tuple[torch.Tensor]] = None,
        attention_mask: Optional[torch.FloatTensor] = None,
        head_mask: Optional[torch.FloatTensor] = None,
        encoder_hidden_states: Optional[torch.Tensor] = None,
        encoder_attention_mask: Optional[torch.FloatTensor] = None,
        use_cache: Optional[bool] = False,
        output_attentions: Optional[bool] = False,
    ) -> Tuple[Union[torch.Tensor, Tuple[torch.Tensor]], ...]:
        if encoder_hidden_states is not None:
            if not hasattr(self, "q_attn"):
                raise ValueError(
                    "If class is used as cross attention, the weights `q_attn` have to be defined. "
                    "Please make sure to instantiate class with `GPT2Attention(..., is_cross_attention=True)`."
                )

            query = self.q_attn(hidden_states)
            key, value = self.c_attn(encoder_hidden_states).split(self.split_size, dim=2)
            attention_mask = encoder_attention_mask
        else:
            query, key, value = self.c_attn(hidden_states).split(self.split_size, dim=2)

        query = self._split_heads(query, self.num_heads, self.head_dim)
        key = self._split_heads(key, self.num_heads, self.head_dim)
        value = self._split_heads(value, self.num_heads, self.head_dim)

        # 过去所存的值
        if layer_past is not None:
            past_key, past_value = layer_past
            key = torch.cat((past_key, key), dim=-2)  # 把当前新的key加入
            value = torch.cat((past_value, value), dim=-2)  # 把当前新的value加入

        if use_cache is True:
            present = (key, value)  # 输出用于保存
        else:
            present = None

        if self.reorder_and_upcast_attn:
            attn_output, attn_weights = self._upcast_and_reordered_attn(query, key, value, attention_mask, head_mask)
        else:
            attn_output, attn_weights = self._attn(query, key, value, attention_mask, head_mask)

        attn_output = self._merge_heads(attn_output, self.num_heads, self.head_dim)
        attn_output = self.c_proj(attn_output)
        attn_output = self.resid_dropout(attn_output)

        outputs = (attn_output, present)
        if output_attentions:
            outputs += (attn_weights,)

        return outputs  # a, present, (attentions)

总的来说, KV Cache是以空间换时间的做法, 通过使用快速的缓存存取, 减少了重复计算。(注意，只有decoder结构的模型可用，因为有mask attention的存在，使得前面的token可以不用关注后面的token)

但是, 用了KV Cache之后也不是立刻万事大吉。

我们简单算一下, 对于输入长度为 $s$, 层数为 $L$, hidden size为 $d$ 的模型, 需要缓存的参数量为

如果使用的是半精度浮点数，那么总共所需的空间就是

以Llama2 7B为例，有 $L=32 ， L=4096$ ，那么每个token所需的缓存空间就是524，288 bytes, 约 52 K , 当 $s=1024$ 时, 则需要 $536,870,912$ bytes, 超过 500 M 的空间。

这里考虑的还只是batch size=1的情况，如果batch size增大，这个值更是很容易就超过1G。

（MHA相比单头的情况，相当于只是把 $q 、 k 、 v$ 切成多份并行计算了，对于实际需要缓存的大小没有影响）

看下现在主流的科学计算卡配置

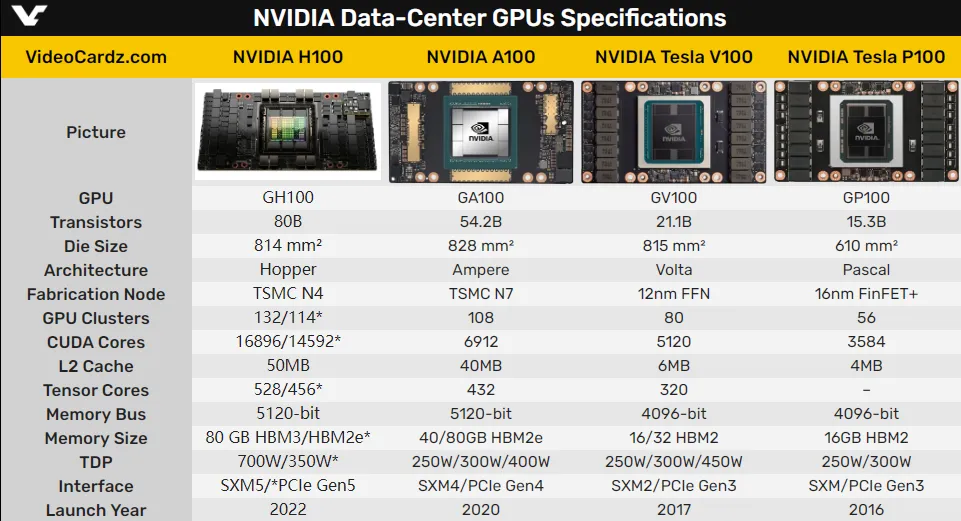
强如H100也只有 $50 M$ 的L2 Cache（L1 Cache的大小更是可以忽略不计），大概只能支持 Llama2 7B总共100个token左右的输入。

想想我们现在用的LLM动辄34B/70B的规模，长度更是以千为基础单位，这样明显是不够用的。

那么超出L2 Cache的部分只能走到显存中去了，但是HBM速度比L2 Cache慢多了。

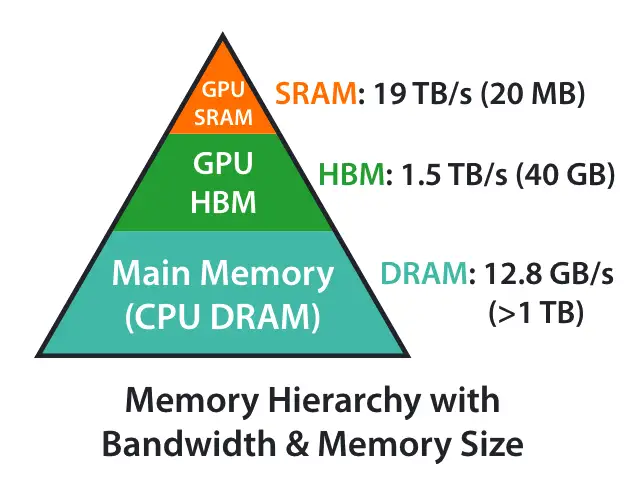
看来还需要进一步优化。

要保证模型的推理加速, 要么增大Cache的大小, 而且是需要一到两个数量级的增强, 那这个只能靠黄老板了。

要么就是减少需要缓存的量。

4.MQA

MQA就是来减少缓存所需要的量的。

Google在2019年就在《Fast Transformer Decoding: One Write-Head is All You Need》提出了 MQA，不过那时候主要到的人不多，那是大家主要还是关注在用Bert把榜刷出新高上。

MQA的做法其实很简单。在MHA中, 输入分别经过 $W_{Q} 、 W_{K} 、 W_{V}$ 的变换之后, 都切成了 n 份 ( $\mathrm{n}=$ 头数)，维度也从 $d_{\text {model }}$ 降到了 $d_{\text {head }}$ ，分别进行attention计算再拼接。而MQA这里，在线性变换之后，只对 $Q$ 进行切分（和MHA一样），而 $K 、 V$ 则直接在线性变换的时候把维度降到了 $d_{\text {head }}$ （而不是切分变小），然后这 n 个Query头分别和同一份 $K 、 V$ 进行attention计算，之后把结果拼接起来。

简单来说，就是MHA中，每个注意力头的 $K 、 V$ 是不一样的，而MQA这里，每个注意力头的 $K 、 V$ 是一样的，值是共享的。而其他步骤都和MHA一样。

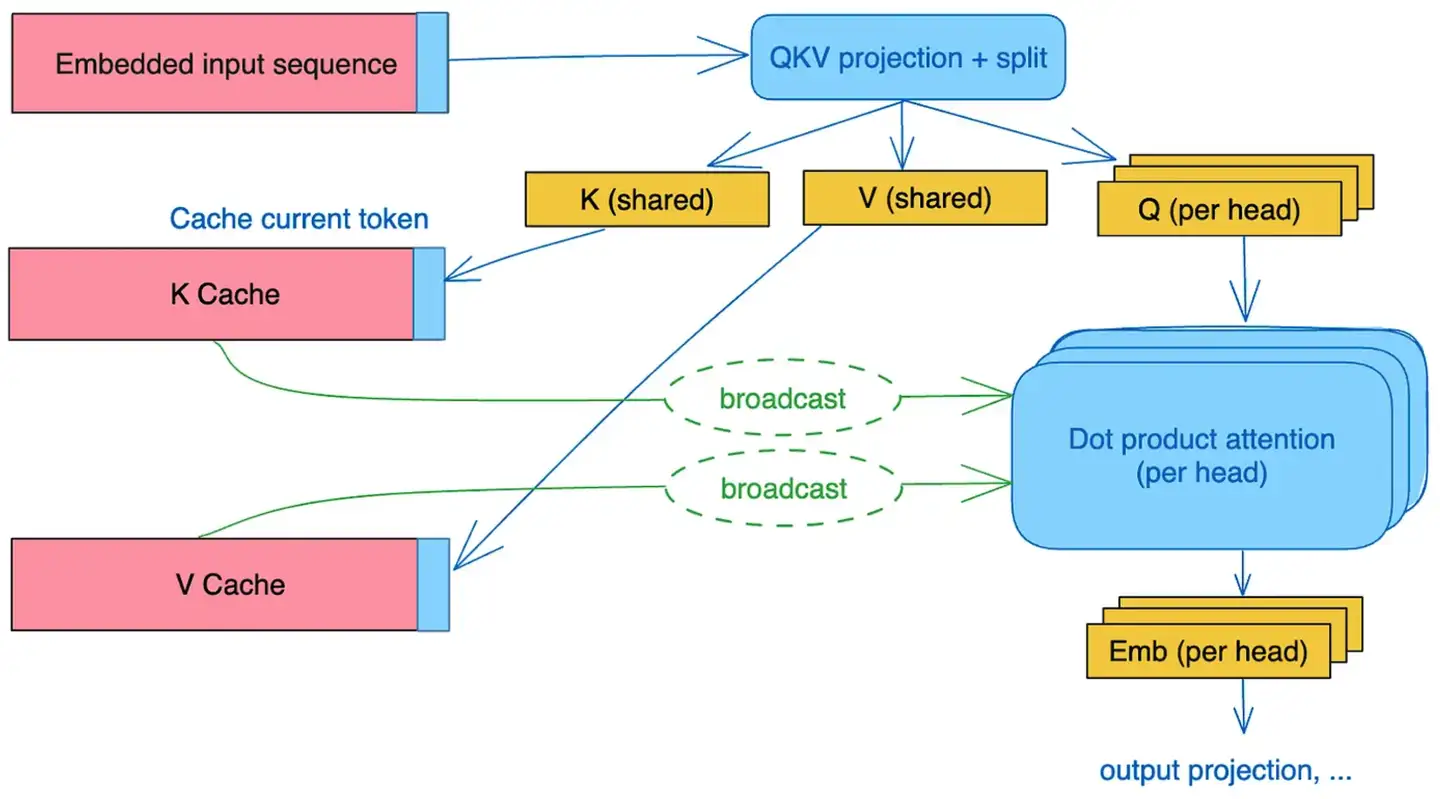
这样一来，需要缓存的 $K 、 V$ 值一下就从所有头变成一个头的量。

比如在Llama2 7B中用的是32个头, 那用MQA后, 1024个token需要缓存的量就变成1/32, $536,870,912$ bytes / $32=16,777,216$ bytes, 差不多是16M, 这就能全塞进缓存中了。

（实现上，就是改一下线性变换矩阵，然后把 $K 、 V$ 的处理从切分变成复制，就不再赘述。）

当然，由于共享了多个头的参数，限制了模型的表达能力，MQA虽然能好地支持推理加速，但是在效果上略略比MHA差一点, 但是并不多, 且相比其他修改hidden size或者head num的做法效果都好。

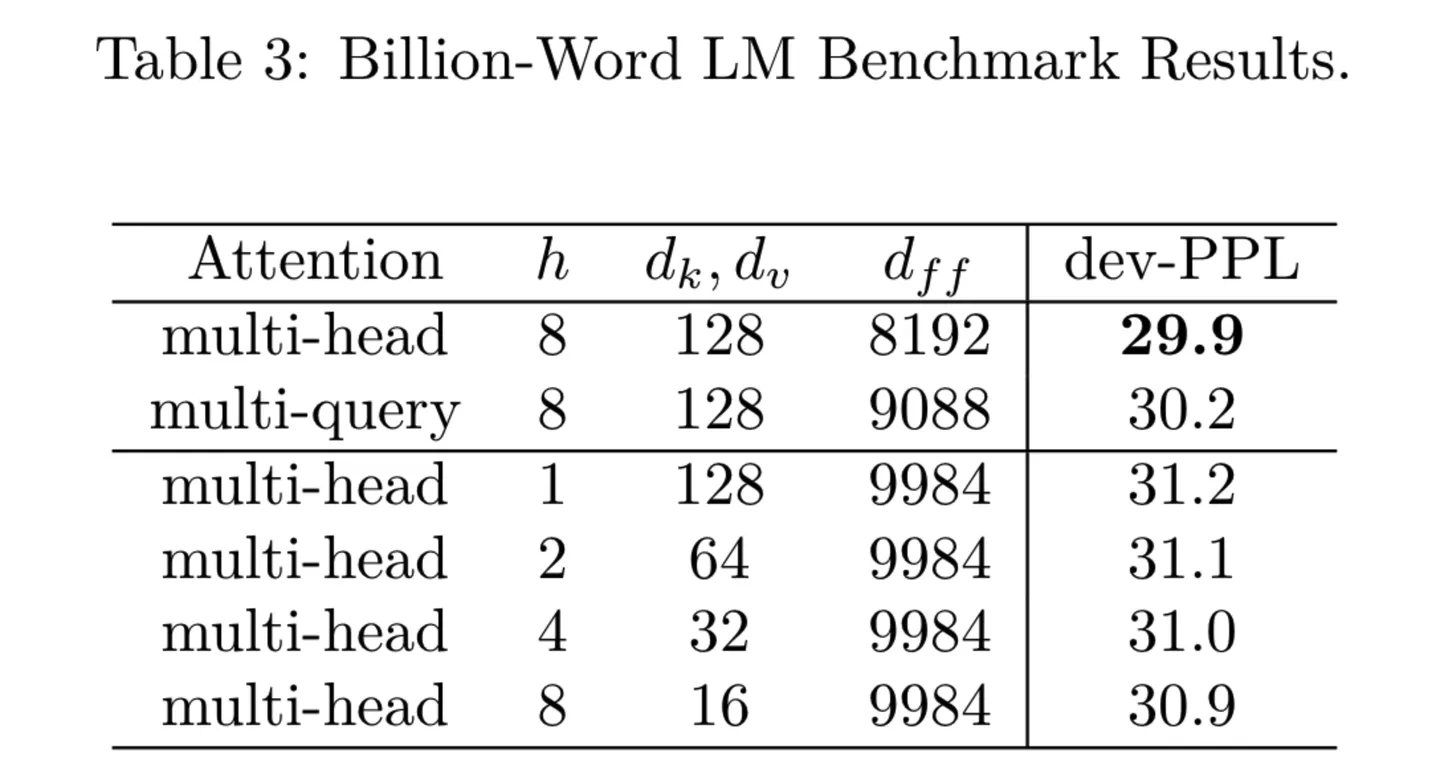
5.GQA

既然MQA对效果有点影响，MHA缓存又存不下，那GQA（Grouped-Query Attention）就提出了一个折中的办法, 既能减少MQA效果的损失, 又相比MHA需要更少的缓存。

（文章：《GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints》, 2023年）

GQA里， $Q$ 还是按原来MHA/MQA的做法不变。只使用一套共享的 $K 、 V$ 不是效果不好吗，那就还是多弄几套。但是不要太多，数量还是比 $Q$ 的头数少一些。这样相当于把 $Q$ 的多个头给分了 group, 同一个group内的 $Q$ 共享同一套 $K 、 V$ ，不同group的 $Q$ 所用的 $K 、 V$ 不同。

MHA可以认为是 $K 、 V$ 头数最大时的GQA, 而MQA可以任务是 $K 、 V$ 头数最少时的GQA。

看论文里的图就很直观

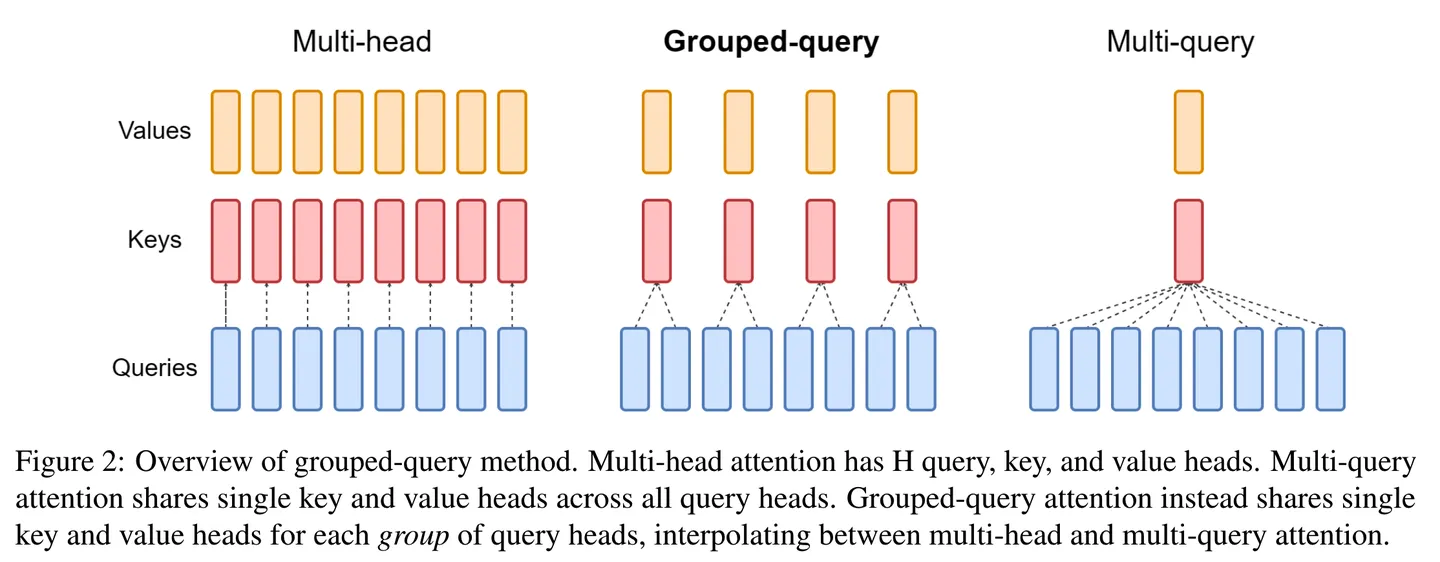
效果怎么样呢?

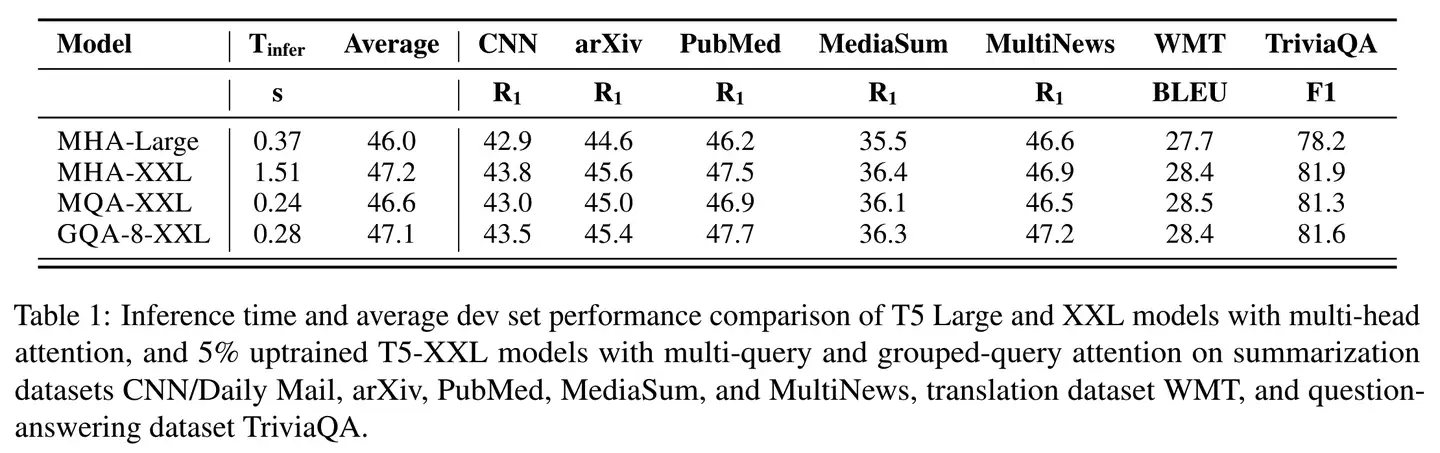
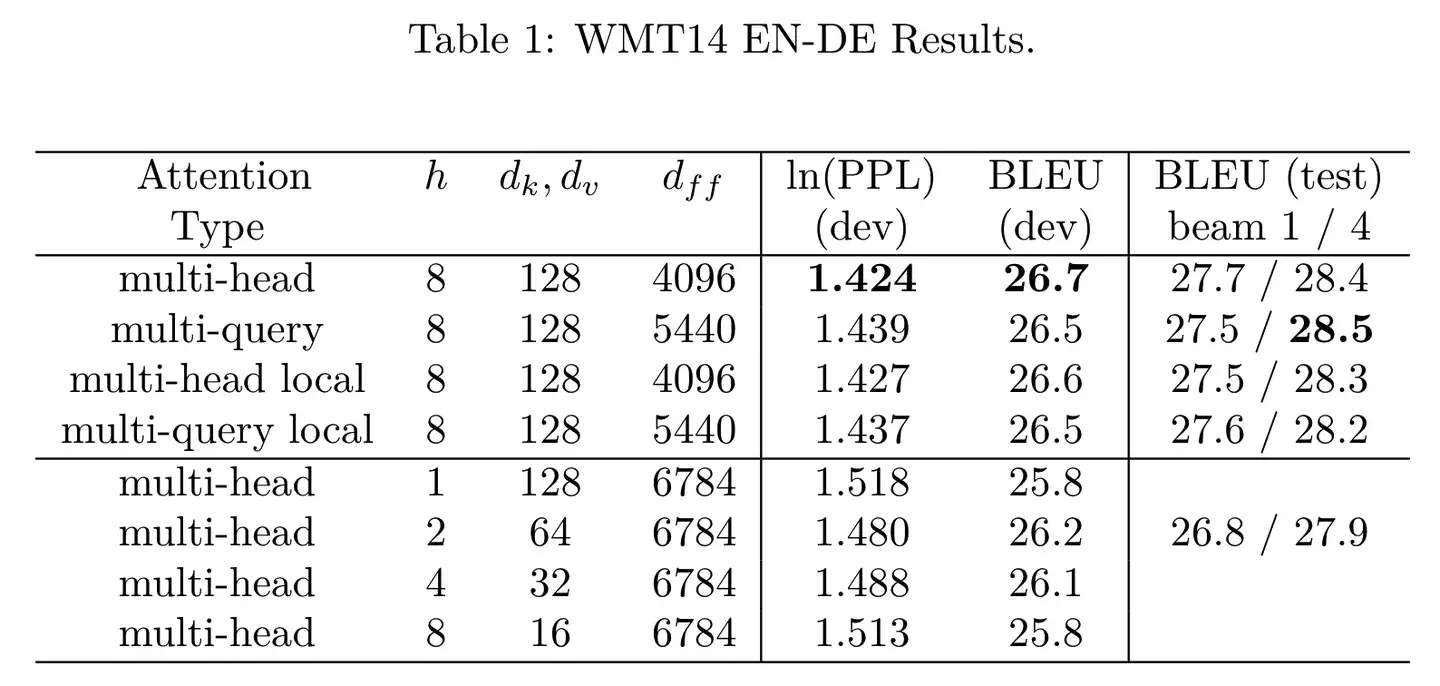
看表中 $2 / 3 / 4$ 行对比，GQA的速度相比MHA有明显提升，而效果上比MQA也好一些，能做到和MHA基本没差距。文中提到，这里的MQA和GQA都是通过average pooling从MHA初始化而来，然后进行了少量的训练得到的。如果我们想要把之前用MHA训练的模型改造成 GQA，也可以通过这样的方法，增加少量训练来实现。当然如果从一开始就加上，从零开始训练，也是没有问题的。

Llama2用的就是GQA，在tech report中也做了MHA、MQA、GQA的效果对比，可以看到效果确实很不错。

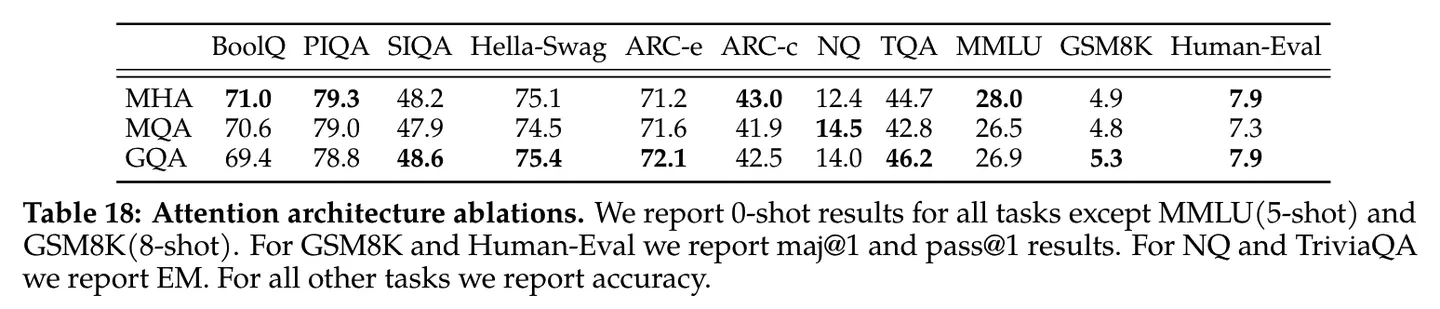
6.小结

MHA、MQA、GQA的实现其实并不复杂，效果也很好，理解上并没有太多困难。但是想要真正理解它们的出发点，还是需要深入每一个细节，去了解当时要解决的事什么问题。

目前来看GQA是LLM比较好的方案，但未来肯定还会有针对不同方向的进一步优化方案，计算效率、推理速度、显存消耗这些方向都值得我们继续去探索优化。