flash attention V1 V2 V3 V4 如何加速 attention，主要包括 flash attention V1 V2 V3 V4 的原理和实现，以及如何加速 attention 的方法。

#! https://zhuanlan.zhihu.com/p/685020608

flash attention V1 V2 V3 V4 如何加速 attention

1. flash attention V1

论文：FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness

链接：https://arxiv.org/abs/2205.14135

1.1 Important

• 为什么加快了计算？Fast
  • 降低了耗时的HBM访问次数。采用Tiling技术分块从HBM加载数据到SRAM进行融合计算。
• 为什么节省了内存？Memory-Efficient
  • 不再对中间矩阵S，P进行存储。在反向的时候通过Recomputation重新计算来计算梯度。
• 为什么是精准注意力？Exact Attention
  • 算法流程只是分块计算，无近似操作。

1.2 Motivation

Transformer 结构已成为自然语言处理和图像分类等应用中最常用的架构。尽管 Transformer 在规模上不断增大和加深，但处理更长上下文仍然是一个挑战，因为核心的自注意力模块在序列长度上具有二次方的时间和内存复杂度。这导致在处理长序列时速度变慢且内存需求巨大。因此，我们需要一些优化算法来提高注意力模块的计算速度和内存利用率。

1.3 Solution

符号定义：

• ${N}$: sequence length
• ${d}$: head dimension
• ${M}$: the size of SRAM
• ${\Omega}$：大于等于的数量级复杂度
• ${O}$：小于等于的数量级复杂度
• ${\Theta}$：同数量级的复杂度
• ${o}$：小于的数量级复杂度

flash attention v1从attention计算的GPU memory的read和write方面入手来提高attention计算的效率。其主要思想是通过切块（tiling）技术，来减少GPU HBM和GPU SRAM之间的数据读写操作。通过切块，flash attention1实现了在BERT-large（seq. length 512)上端到端15%的提速，在GPT-2（seq. length 1k)上3x的提速。具体数据可看flash attention 1的paper。

NVIDIA GPU的显存架构，左图是以NVIDIA A100 40G显卡为例，我们常说的40G显存是其HBM memory（high bandwidth memory），其带宽是1.5~2.0TB/s，A100上还有一块192KB每108 SM (streaming multiprocessors) 的on-chip SRAM memory，其带宽是19TB/s。因此，如果能把涉及到显存的读写操作放在SRAM上，那将会极大的提升速度。

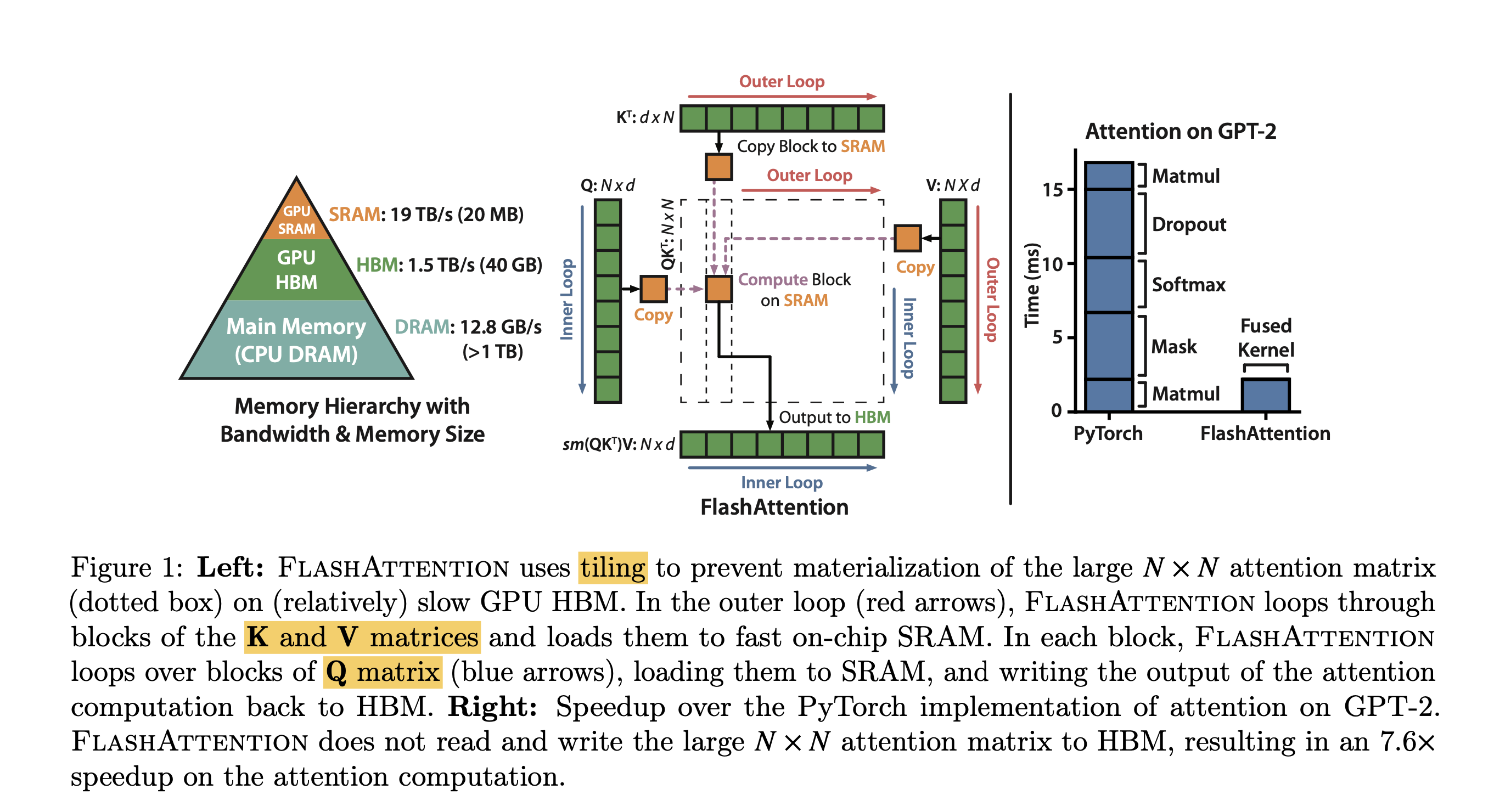
Forward Standard Attention Implementation

在注意力的一般实现中, 对 $\mathbf{Q}, \mathbf{K}, \mathbf{V} \in \mathbb{R}^{N \times d}$ 三个输入执行以下算法得到输出 $\mathbf{O}$, 其中softmax行级别执行。

在这个算法中, $\mathbf{S}, \mathbf{P}$ 矩阵都是很大, 需要在 HBM中实例化来进行存储, 这样就会带来很多HBM的访问次数, 最终体现到算法时间端到端较长的延迟。

FlashAttention Implementation(Tiling)

理论基础

在传统算法中, 一种方式是将Mask和SoftMax部分融合, 以减少访存次数。然而, FlashAttention则更加激进,它将从输入 $\mathbf{Q}, \mathbf{K}, \mathbf{V}$ 到输出 $\mathbf{O}$ 的整个过程进行融合, 以避免 $\mathbf{S}, \mathbf{P}$ 矩阵的存储开销, 实现喘到端的延迟经減。然而,由于输入的长度 $N$ 通常很长, 无法完全将完整的 $\mathbf{Q}, \mathbf{K}, \mathbf{V}, \mathbf{O}$ 及中间计算结果存储在SRAM中。因此, 需要依赖HBM 进行访存操作, 与原始计算延迟相比没有太大差异, 甚至会变慢。

为了让计算过程的结果完全在SRAM中, 摆脱对HBM的依赖, 可以采用分片操作, 每次进行部分计算, 确保这些计算结果能在SRAM内进行交互, 待得到对应的结果后再进行输出。

这个过程中, 有一点需要注意的是, 之前对于softmax的计算是以行为单位的, 如下所示:

当我们将输入进行分片后，无法对完整的行数据执行Softmax操作。这是因为Softmax函数在计算时需要考虑整个行的数据。然而, 我们可以通过如下所示方法来获得与完整行Softmax相同的结果, 而无需使用近似操作。

flash attention v1的forward实现:

这个算法图的大致流程可以理解成把大块的Q和KV矩阵分成小块，一个一个小块搬到SRAM上计算然后再把结果写回HBM中，在计算attention分数的时候就把最终输出计算出来，不维护中间的N*N attention分数矩阵。

上图算法流程是flash attention1的forward实现。我们逐步的看一下计算过程。

1. 首先根据SRAM的大小, 计算出合适的分块block大小;
2. 将 $O, l, m$ 在HBM中初始化为对应shape的全 0 的矩阵或向量, $l, m$ 的具体作用后面算法流程会说明;
3. 将 $Q, K, V$ 按照分块block的大小切分成许多个blocks;
4. 将 $O, l, m$ 也切分成对应数量的blocks;
5. 执行outer loop, 在outer loop中, 做的IO操作是将分块的 $K_j, V_j$ 从HBM中加载到SRAM中;
6. 执行inner loop, 将 $Q_i, O_i, l_i, m_i$ 从HBM中load到SRAM中, 然后分块计算上面流程的中间值, 在每个inner loop里面, 都将 $O_i, l_i, m_i$ 写回到HBM中, 因此与HBM的IO操作还是相对较多的。

由于我们将 $Q, K, V$ 都进行了分块计算, 而softmax 却是针对整个vector执行计算的, 因此在上图flash attention的计算流程的第 10 、 11、12步中, 其使用了safe online softmax技术。 $y=\operatorname{softmax}(x)$ 的定义为

Algorithm 1 Naive softmax

• $d_0 \leftarrow 0$
• for $j \leftarrow 1, V$ do
  • $d_j \leftarrow d_{j-1}+e^{x_j}$
• end for
• for $i \leftarrow 1, V$ do
  • $y_i \leftarrow \frac{e^{x_i}}{d_V}$
• end for

上面是naive softmax的实现过程, 首先需要迭代计算分母的和, 然后再迭代计算vector中每一个值对应的softmax值。这个过程需要两次从内存读取和一次写回内存操作。

但是naive softmax在实际的硬件上计算是有问题的, 在naive softmax的实现过程的第3步, 由于有指数操作, 会有数值溢出的情况, 因此在实际使用时, softmax都是使用safe softmax算法

Algorithm 2 Safe softmax

• $m_0 \leftarrow-\infty$
• for $k \leftarrow 1, V$ do
  • $m_k \leftarrow \max \left(m_{k-1}, x_k\right)$
• end for
• $d_0 \leftarrow 0$
• for $j \leftarrow 1, V$ do
  • $d_j \leftarrow d_{j-1}+e^{x_j-m_V}$
• end for
• for $i \leftarrow 1, V$ do
  • $y_i \leftarrow \frac{e^{x_i-m_V}}{d_V}$
• end for

上面是safe softmax的计算过程, 其主要修改是在指数部分, 减去了要计算vector的最大值, 保证了指数部分的最大值是 0 , 避免了数值溢出。在几乎所有的深度学习框架中, 都是使用safe softmax来执行softmax算法的。但是safe softmax相比naive softmax, 多了一次数据的读取过程, 总共是从内存中有三次读取, 一次写入操作。

但是不管是naive softmax还是safe softmax, 都需要传入一整个vector进行计算, 但是flash attention v1 算法执行了分块（tiling）策略, 导致不能一次得到整个vector, 因此需要使用online safe softmax算法。

Algorithm 3 Safe softmax with online normalizer calculation

• $m_0 \leftarrow-\infty$
• $d_0 \leftarrow 0$
• for $j \leftarrow 1, V$ do
  • $m_j \leftarrow \max \left(m_{j-1}, x_j\right)$
  • $d_j \leftarrow d_{j-1} \times e^{m_{j-1}-m_j}+e^{x_j-m_j}$
• end for
• for $i \leftarrow 1, V$ do
  • $y_i \leftarrow \frac{e^{x_i-m_V}}{d_V}$
• end for

上面的算法流程是online safe softmax的计算过程。在safe softmax中, vector的最大值 $m$ 的计算是在一个单独的for循环中, 在online safe softmax中, $m$ 的计算是迭代进行的, 因此得到的 $m$ 不是一个vector中最大的值, 而是迭代过程中的局部极大值, 相应的对softmax的分母 $d$ 的计算也要加一个补偿项 $e^{m_{j-1}-m_j}$ 。

这样得出的结果与直接使用safe softmax是一致的, 具体的证明过程可以参考论文Online normalizer calculation for softmax。链接：https://arxiv.org/abs/1805.02867。

在flash attention v1的算法中，其也使用了online safe softmax，并对其算法进行了相应的扩展。

具体的分块softmax代码演示

• 代码demo

import torch
q = torch.tensor([1,2]).float()
v = torch.tensor([1,2]).float()
print(q)
print(v)

q_sm = torch.softmax(q, 0)
print(q_sm)

result = torch.dot(q_sm, v)
print(result)


"""
This code calculates the softmax function for a sequence of blocks.
It iterates through each block and updates the current sum based on the softmax calculation.

The steps involved in the calculation are as follows:
1. Get the maximum value between the current block and the previous block's maximum value.
2. Scale the previous block's log value by the difference between the maximum values.
3. Calculate the exponential values for the current block and compute the current log sum.
4. Scale the previous result by the ratio of the previous log sum and the current log sum.
5. Calculate the proportion of the current probability in the overall sum.
6. Update the current result.

The final result is printed after each block iteration.
"""

m_pre = float("-inf")  # 前一个块的最大值
l_pre = 0  # 前一个块的对数值
cur_sum = 0  # 存储当前的结果

block1 = torch.tensor([1]).float()
# get cur max value
# 1. 获取 block1 和前一个块的最大值 m_pre 中的最大值 m_cur。这是为了在后续的计算中防止指数运算的溢出。
m_cur = max(torch.max(block1), m_pre)
# scale pre log value by max exp， 对前一个block的log值进行缩放
# 2. 前一个块的对数值 l_pre 进行缩放。这是通过将 l_pre 乘以 m_pre 和 m_cur 的差的指数实现的。
l_pre *= torch.exp(m_pre - m_cur)
# calculate current log sum
# 3. 计算当前块的指数值，并通过 l_cur = torch.sum(p) + l_pre 计算当前的对数和 l_cur。
p = torch.exp(block1 - m_cur)
l_cur = torch.sum(p) + l_pre
# scale pre result by log sum
# 4. 对前一个结果 cur_sum 进行缩放。这是通过将 cur_sum 乘以 l_pre 和 l_cur 的比值实现的。
cur_sum = cur_sum * l_pre / l_cur
# 5. 计算当前的概率 p 在整体求和中的比例。
p = p / l_cur # 当前的P在整体求和当中的比例
# 6. 更新当前的结果 cur_sum
cur_sum = 1 * p[0]


l_pre = l_cur
m_pre = m_cur

print(cur_sum)


block2 = torch.tensor([2]).float()
# 1. 获取 block2 和前一个块的最大值 m_pre 中的最大值 m_cur。这是为了在后续的计算中防止指数运算的溢出。
m_cur = max(torch.max(block2), m_pre)
# 2. 对前一个块的对数值 l_pre 进行缩放。这是通过将 l_pre 乘以 m_pre 和 m_cur 的差的指数实现的。
l_pre *= torch.exp(m_pre - m_cur)
# 3. 计算当前块的指数值，并通过 l_cur = torch.sum(p) + l_pre 计算当前的对数和 l_cur。
p = torch.exp(block2 - m_cur)
l_cur = torch.sum(p) + l_pre
# 4. 对前一个结果 cur_sum 进行缩放。这是通过将 cur_sum 乘以 l_pre 和 l_cur 的比值实现的。
cur_sum = cur_sum * l_pre / l_cur
# 5.  计算当前的概率 p 在整体求和中的比例。
p = p / l_cur
# 6. 更新当前的结果 cur_sum
cur_sum += 2 * p[0]

print(cur_sum)


# tensor([1., 2.])
# tensor([1., 2.])
# tensor([0.2689, 0.7311])
# tensor(1.7311)
# tensor(1.)
# tensor(1.7311)

代码实现

链接：https://github.com/openai/triton/blob/main/python/tutorials/06-fused-attention.py#L17

@triton.jit
def _fwd_kernel(
    Q, K, V, sm_scale,
    L, M,
    Out,
    stride_qz, stride_qh, stride_qm, stride_qk,
    stride_kz, stride_kh, stride_kn, stride_kk,
    stride_vz, stride_vh, stride_vk, stride_vn,
    stride_oz, stride_oh, stride_om, stride_on,
    Z, H, N_CTX,
    BLOCK_M: tl.constexpr, BLOCK_DMODEL: tl.constexpr,
    BLOCK_N: tl.constexpr,
):
    start_m = tl.program_id(0)
    off_hz = tl.program_id(1)
    # initialize offsets
    offs_m = start_m * BLOCK_M + tl.arange(0, BLOCK_M)
    offs_n = tl.arange(0, BLOCK_N)
    offs_d = tl.arange(0, BLOCK_DMODEL)
    off_q = off_hz * stride_qh + offs_m[:, None] * stride_qm + offs_d[None, :] * stride_qk
    off_k = off_hz * stride_qh + offs_n[None, :] * stride_kn + offs_d[:, None] * stride_kk
    off_v = off_hz * stride_qh + offs_n[:, None] * stride_qm + offs_d[None, :] * stride_qk
    # Initialize pointers to Q, K, V
    q_ptrs = Q + off_q
    k_ptrs = K + off_k
    v_ptrs = V + off_v
    # initialize pointer to m and l
    m_prev = tl.zeros([BLOCK_M], dtype=tl.float32) - float("inf")
    l_prev = tl.zeros([BLOCK_M], dtype=tl.float32)
    acc = tl.zeros([BLOCK_M, BLOCK_DMODEL], dtype=tl.float32)
    # load q: it will stay in SRAM throughout
    q = tl.load(q_ptrs)
    # loop over k, v and update accumulator
    for start_n in range(0, (start_m + 1) * BLOCK_M, BLOCK_N):
        # -- compute qk ----
        k = tl.load(k_ptrs)
        qk = tl.zeros([BLOCK_M, BLOCK_N], dtype=tl.float32)
        qk += tl.dot(q, k)
        qk *= sm_scale
        qk = tl.where(offs_m[:, None] >= (start_n + offs_n[None, :]), qk, float("-inf"))
        # compute new m
        m_curr = tl.maximum(tl.max(qk, 1), m_prev)
        # correct old l
        l_prev *= tl.exp(m_prev - m_curr)
        # attention weights
        p = tl.exp(qk - m_curr[:, None])
        l_curr = tl.sum(p, 1) + l_prev
        # rescale operands of matmuls
        l_rcp = 1. / l_curr
        p *= l_rcp[:, None]
        acc *= (l_prev * l_rcp)[:, None]
        # update acc
        p = p.to(Q.dtype.element_ty)
        v = tl.load(v_ptrs)
        acc += tl.dot(p, v)
        # update m_i and l_i
        l_prev = l_curr
        m_prev = m_curr
        # update pointers
        k_ptrs += BLOCK_N * stride_kn
        v_ptrs += BLOCK_N * stride_vk
    # rematerialize offsets to save registers
    start_m = tl.program_id(0)
    offs_m = start_m * BLOCK_M + tl.arange(0, BLOCK_M)
    # write back l and m
    l_ptrs = L + off_hz * N_CTX + offs_m
    m_ptrs = M + off_hz * N_CTX + offs_m
    tl.store(l_ptrs, l_prev)
    tl.store(m_ptrs, m_prev)
    # initialize pointers to output
    offs_n = tl.arange(0, BLOCK_DMODEL)
    off_o = off_hz * stride_oh + offs_m[:, None] * stride_om + offs_n[None, :] * stride_on
    out_ptrs = Out + off_o
    tl.store(out_ptrs, acc)

1.4 IO Complexity Analysis

Standard Attention

对于标准注意力实现, 初期我们需要把输入 $\mathbf{Q}, \mathbf{K}, \mathbf{V}$ 从 HBM中读取, 并计算完毕后把输出 $\mathbf{O}$ 写入到HBM中。

第一步把 $\mathbf{Q}, \mathbf{K}$ 读职出来计算出 $\mathbf{S}=\mathbf{Q} \mathbf{K}^{\top}$, 然后把 $\mathbf{S}$ 存回去, 内存访问复杂度 $\Theta\left(N d+N^2\right)$ 。

第二步把 $\mathbf{S}$ 读取出来计算出 $\mathbf{P}=\operatorname{softmax}(\mathbf{S})$, 然后把 $\mathbf{P}$ 存回去, 内存访问复杂度 $\Theta\left(N^2\right)$ 。

第三步把 $\mathbf{V}, \mathbf{P}$ 读取出来计算出 $\mathbf{O}=\mathbf{P V}$, 然后计算出结果 $\mathbf{O}$, 内存访问复杂度 $\Theta\left(N d+N^2\right)$ 。

综上所述, 整体的内存访问复杂度为 $\Theta\left(N d+N^2\right)$ 。

FlashAttention

对于FlashAttention, 我们设置一个分块大小 $B_c$ 来把 $\mathbf{K}, \mathbf{V}$ 分成 $T_c$ 块，对于 $\mathbf{Q}, \mathbf{O}$ 的每一块都要把 $\mathbf{K}, \mathbf{V}$ 部分的全部元素Load一遍，这样则有FlashAttention的内存访问复杂度为 $\Theta\left(N d+N d T_c\right)=\Theta\left(N d T_c\right)$.

在这里, 我们需要两个分块大小, $\mathbf{Q}, \mathbf{O}$ 的分块大小 $B_r, \mathbf{K}, \mathbf{V}$ 的分块大小 $B_c$, 我们设定SRAM的大小为 $M$ , 为了能把分块后的 $\mathbf{K}, \mathbf{V} \in \mathbb{R}^{B_c \times d}$ 放进 $S R A M$, 那么则有一下限制:

相应的， $\mathbf{Q}, \mathbf{O} \in \mathbb{R}^{B_r \times d}$ 有如下限制:

最终, 还有一个中间态 $\mathbf{S}=\mathbf{Q} \mathbf{K}^{\top} \in \mathbb{R}^{B_r \times B_c}$ 需要存储, 则有如下限制:

综上, 限制如下

进而推出

那么在 $M=\Theta(N d)$ 的前提下，则有FlashAttention的HBM内存访问复杂度为：

在语言建模中, 通常有 $d \ll N$, 则有 $\Theta_{\text {stand }}\left(N d+N^2\right)>\Theta_{\text {flash }}(N d)$ 。这样, 在前向的过程中, 我们采用分块计算的方式, 避免了 $\mathbf{S}, \mathbf{P}$ 矩阵的存储开销, 整体的运算都在SRAM内进行, 降低了HBM访问次数, 大大提升了计算的速度, 减少了对存储的消耗。

反向传播需要重新计算${P}$和${S}$，增加了运算量但是减少了HBM访问次数，仍旧快于标准attention。

2. flash attention V2

论文：FlashAttention-2- Faster Attention with Better Parallelism and Work Partitioning

链接：https://arxiv.org/abs/2307.08691

在过去几年中，如何扩展Transformer使之能够处理更长的序列一直是一个重要问题，因为这能提高Transformer语言建模性能和高分辨率图像理解能力，以及解锁代码、音频和视频生成等新应用。然而增加序列长度，注意力层是主要瓶颈，因为它的运行时间和内存会随序列长度的增加呈二次（平方）增加。FlashAttention利用GPU非匀称的存储器层次结构，实现了显著的内存节省（从平方增加转为线性增加）和计算加速（提速2-4倍），而且计算结果保持一致。但是，FlashAttention仍然不如优化的矩阵乘法（GEMM）操作快，只达到理论最大FLOPs/s的25-40%。作者观察到，这种低效是由于GPU对不同thread blocks和warps工作分配不是最优的，造成了利用率低和不必要的共享内存读写。因此，本文提出了FlashAttention-2以解决这些问题。

本文主要贡献和创新点为：

• 减少了non-matmul FLOPs的数量（消除了原先频繁rescale）。虽然non-matmul FLOPs仅占总FLOPs的一小部分，但它们的执行时间较长，这是因为GPU有专用的矩阵乘法计算单元，其吞吐量高达非矩阵乘法吞吐量的16倍。因此，减少non-matmul FLOPs并尽可能多地执行matmul FLOPs非常重要。
• 提出了在序列长度维度上并行化。该方法在输入序列很长（此时batch size通常很小）的情况下增加了GPU利用率。即使对于单个head，也在不同的thread block之间进行并行计算。
• 在一个attention计算块内，将工作分配在一个thread block的不同warp上，以减少通信和共享内存读/写。

FlashAttention V1

FlashAttention应用了tiling技术来减少内存访问，具体来说：

从HBM中加载输入数据（K，Q，V）的一部分到SRAM中，计算这部分数据的Attention结果，更新输出到HBM，但是无需存储中间数据S和P。下图展示了一个示例：首先将K和V分成两部分（K1和K2，V1和V2，具体如何划分根据数据大小和GPU特性调整），根据K1和Q可以计算得到S1和A1，然后结合V1得到O1。接着计算第二部分，根据K2和Q可以计算得到S2和A2，然后结合V2得到O2。最后O2和O1一起得到Attention结果。

值得注意的是，输入数据K、Q、V是存储在HBM上的，中间结果S、A都不需要存储到HBM上。通过这种方式，FlashAttention可以将内存开销降低到线性级别，并实现了2-4倍的加速，同时避免了对中间结果的频繁读写，从而提高了计算效率。

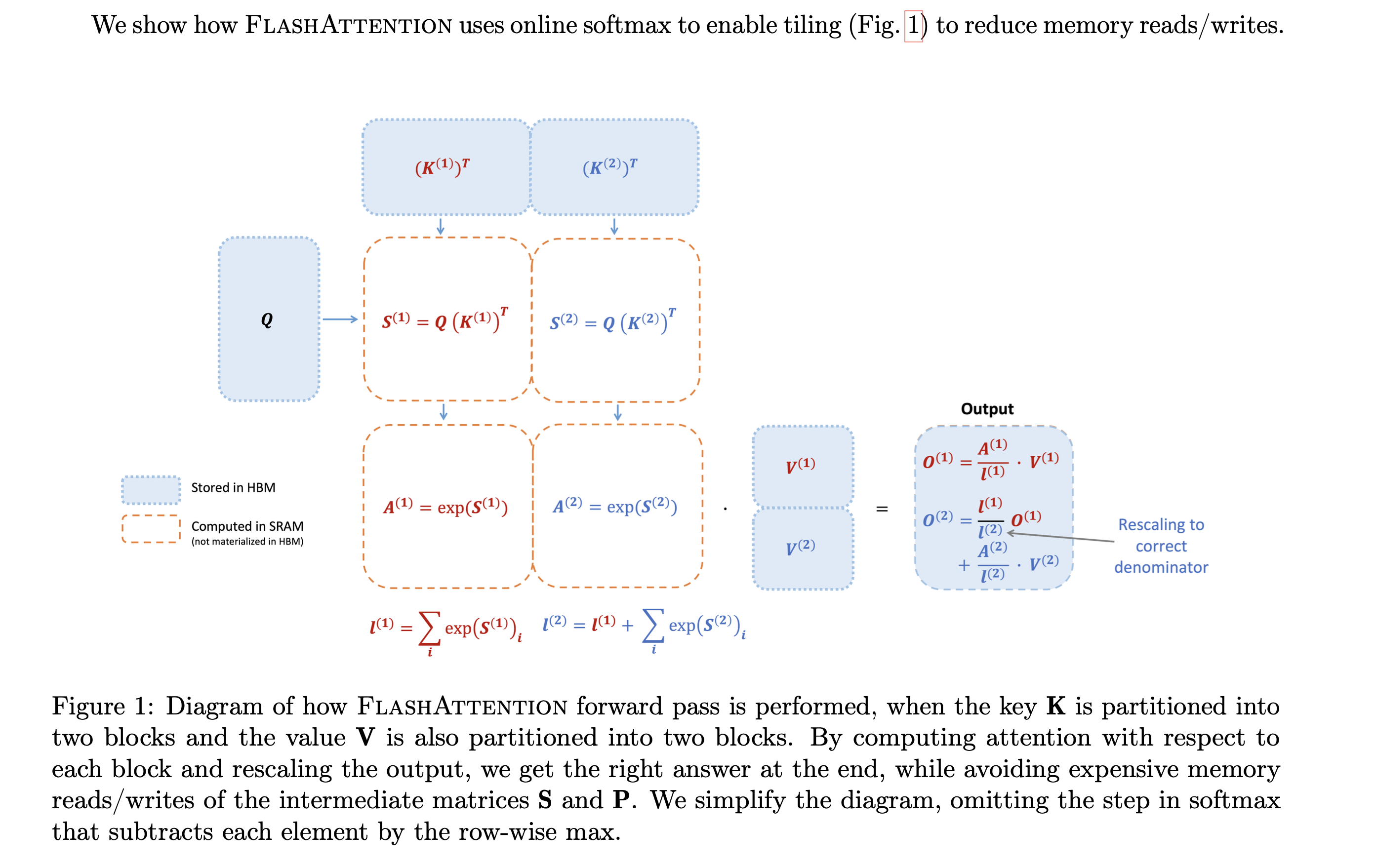
FlashAttention V2

• 先讲述FlashAttention-2对FlashAttention的改进，减少了非矩阵乘法运算（non-matmul）的FLOPs。
• 然后说明如何将任务分配给不同的thread block进行并行计算，充分利用GPU资源。
• 最后描述了如何在一个thread block内部分配任务给不同的warps，以减少访问共享内存次数。这些优化方案使得FlashAttention-2的性能提升了2-3倍。

2.1 Algorithm

FlashAttention在FlashAttention算法基础上进行了调整，减少了非矩阵乘法运算（non-matmul）的FLOPs。这是因为现代GPU有针对matmul（GEMM）专用的计算单元（如Nvidia GPU上的Tensor Cores），效率很高。以A100 GPU为例，其FP16/BF16矩阵乘法的最大理论吞吐量为312 TFLOPs/s，但FP32非矩阵乘法仅有19.5 TFLOPs/s，即每个no-matmul FLOP比mat-mul FLOP昂贵16倍。为了确保高吞吐量（例如超过最大理论TFLOPs/s的50％），我们希望尽可能将时间花在matmul FLOPs上。

2.2 Forward pass

通常实现Softmax算子为了数值稳定性（因为指数增长太快, 数值会过大甚至溢出）, 会减去最大值:

这样带来的代价就是要对 $x$ 遍历 3 次。

为了减少non-matmul FLOPs, 本文在FlashAttention基础上做了两点改进:

1. 在计算局部attention时, 先不考虑softmax的分母 $\sum e^{x_i}$, 即 $\ell^{(i+1)}=e^{m^{(i)}-m^{(i+1)}} \ell^{(i)}+\operatorname{rowsum}\left(e^{\mathbf{S}^{(i+1)}-m^{(i+1)}}\right)$, 例如计算 $\mathbf{O}^{(1)}$ 时去除了 $\operatorname{diag}\left(\ell^{(1)}\right)^{-1}$

   • FlashAttention: $\mathbf{O}^{(1)}=\tilde{\mathbf{P}}(1) \mathbf{V}^{(1)}=\operatorname{diag}\left(\ell^{(1)}\right)^{-1} e^{\mathbf{S}^{(1)}-m^{(1)}} \mathbf{V}^{(1)}$
   • FlashAttention-2: $\mathbf{O}^{(1)}=e^{\mathbf{S}^{(1)}-m^{(1)}} \mathbf{V}^{(1)}$

2. 由于去除了 $\operatorname{diag}\left(\ell^{(i)}\right)^{-1}$, 更新 $\mathbf{O}^{(i+1)}$ 时不需要rescale $\ell^{(i)} / \ell^{(i+1)}$, 但是得弥补之前局部 max值, 例如示例中:

   • FlashAttention: $\mathbf{O}^{(2)}=\operatorname{diag}\left(\ell^{(1)} / \ell^{(2)}\right)^{-1} \mathbf{O}^{(1)}+\operatorname{diag}\left(\ell^{(2)}\right)^{-1} e^{\mathbf{S}^{(2)}-m^{(2)}} \mathbf{V}^{(2)}$
   • FlashAttention-2: $\tilde{\mathbf{O}}^{(2)}=\operatorname{diag}\left(e^{m^{(1)}-m^{(2)}}\right) \tilde{\mathbf{O}}^{(1)}+e^{\mathbf{S}^{(2)}-m^{(2)}} \mathbf{V}^{(2)}=e^{s^{(1)}-m} \mathbf{V}^{(1)}+e^{s^{(2)}-m} \mathbf{V}^{(2)}$

3. 由于更新 $\mathbf{O}^{(i+1)}$ 未进行rescale, 最后一步时需要将 $\tilde{\mathbf{O}}^{(\text {last })}$ 乘以 $\operatorname{diag}\left(\ell^{(\text {last })}\right)^{-1}$ 来得到正确的输出, 例如示例中:

   • FlashAttention-2: $\mathbf{O}=\operatorname{diag}\left(\ell^{(2)}\right)^{-1} \tilde{\mathbf{O}}^{(2)}$

简单示例的FlashAttention完整计算步骤:

FlashAttention-2的完整计算步骤:

再看下面FlashAttention v2 forward pass伪代码：

Causal masking是attention的一个常见操作，特别是在自回归语言建模中，需要对注意力矩阵S应用因果掩码（即任何S ，其中 > 的条目都设置为−∞）。

• 由于FlashAttention和FlashAttention-2已经通过块操作来实现，对于所有列索引都大于行索引的块（大约占总块数的一半），我们可以跳过该块的计算。这比没有应用因果掩码的注意力计算速度提高了1.7-1.8倍。
• 不需要对那些行索引严格小于列索引的块应用因果掩码。这意味着对于每一行，我们只需要对1个块应用因果掩码。

2.3 Parallelism

FlashAttention在batch和heads两个维度上进行了并行化：使用一个thread block来处理一个attention head，总共需要thread block的数量等于batch size × number of heads。每个block被调到到一个SM上运行，例如A100 GPU上有108个SMs。当block数量很大时（例如≥80），这种调度方式是高效的，因为几乎可以有效利用GPU上所有计算资源。

但是在处理长序列输入时，由于内存限制，通常会减小batch size和head数量，这样并行化成都就降低了。因此，FlashAttention-2还在序列长度这一维度上进行并行化，显著提升了计算速度。此外，当batch size和head数量较小时，在序列长度上增加并行性有助于提高GPU占用率。

Forward pass. FlashAttention算法有两个循环，K V 在外循环 j，Q O在内循环 i。FlashAttention-2将 Q 移到了外循环 i，K V 移到了内循环 j，由于改进了算法使得warps之间不再需要相互通信去处理 ${Q_i}$，所以外循环可以放在不同的thread block上。这个交换的优化方法是由Phil Tillet在Triton[17]提出并实现的。

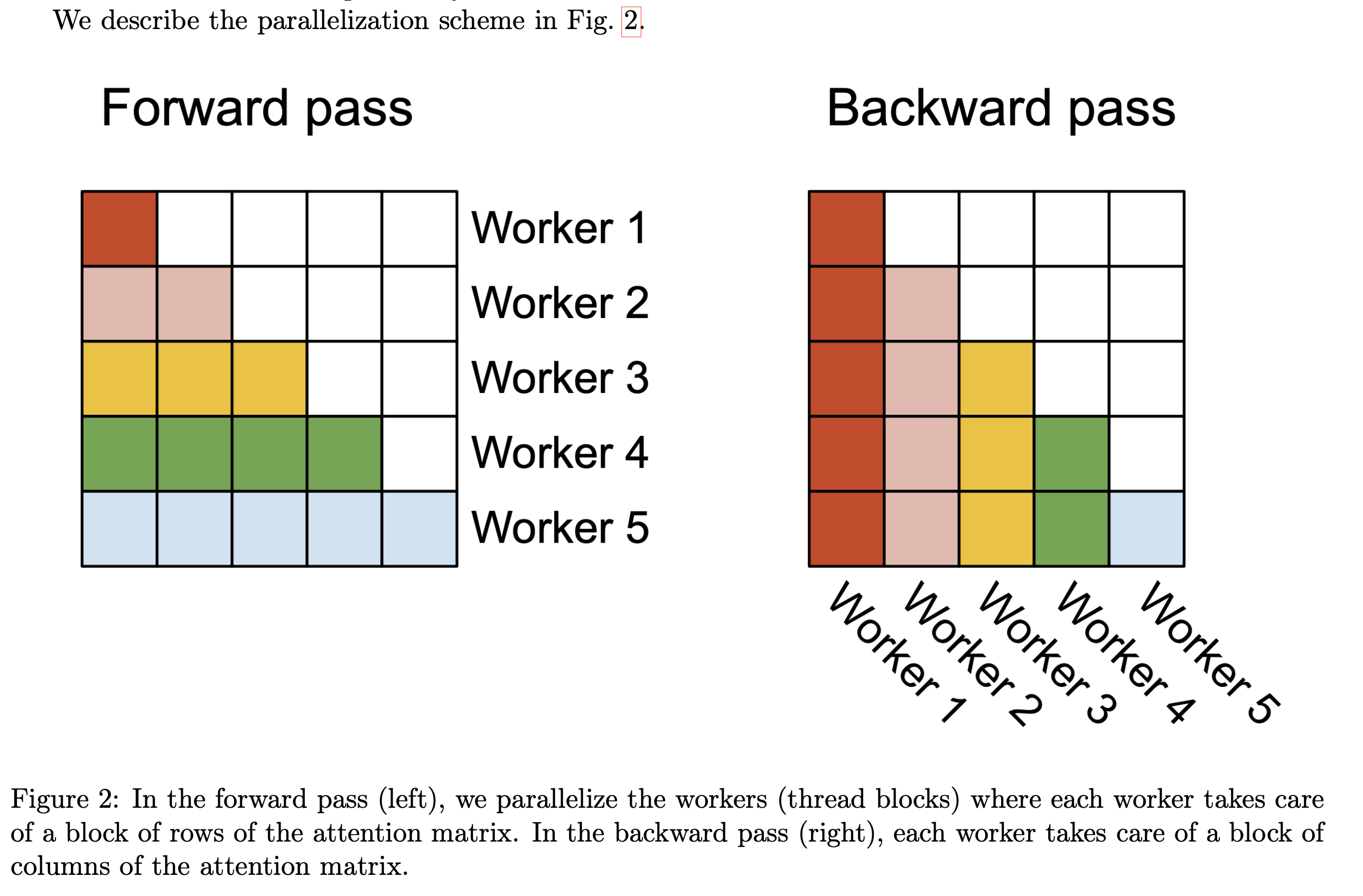
2.4 Work Partitioning Between Warps

上一节讨论了如何分配thread block，然而在每个thread block内部，我们也需要决定如何在不同的warp之间分配工作。我们通常在每个thread block中使用4或8个warp，如下图所示。

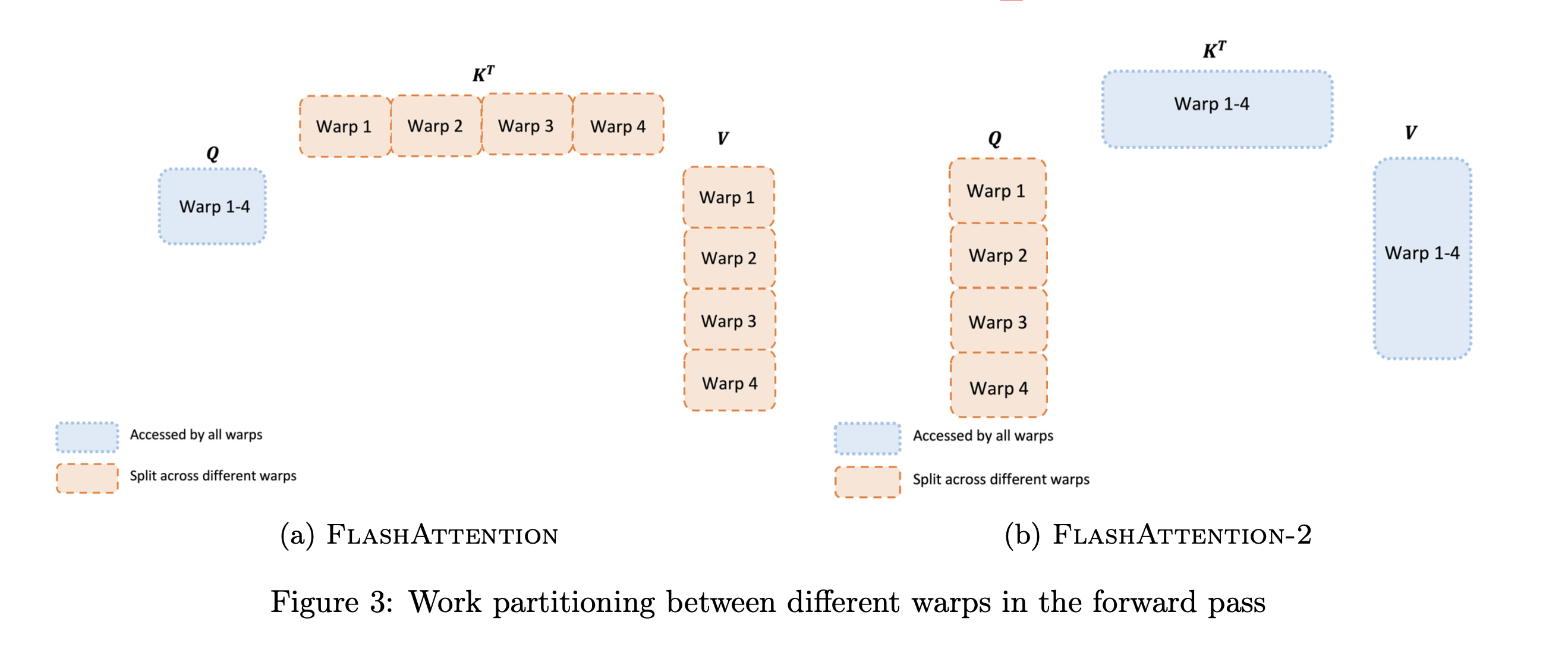
FlashAttention forward pass. 如图所示，外循环对 K V 在输入序列 N上遍历，内循环对 Q 在 N 上遍历。对于每个block，FlashAttention将 K 和 V 分别分为4个warp，并且所有warp都可以访问 Q。K 的warp乘以 Q 得到 S 的一部分 ${S_{ij}}$，然后 ${S_{ij}}$ 经过局部 softmax后还需要乘以 V 的一部分得到 ${O_i}$。然而，每次外循环 j++ 都需要更新一遍 ${O_i}$（对上一次 ${O_i}$ 先rescale再加上当前值），这就导致每个warp需要从HBM频繁读写 ${O_i}$ 以累加出总结果。这种方式被称为“split-K”方案，是非常低效的，因为所有warp都需要从HBM频繁读写中间结果（ ${Q_i}$, ${O_i}$, ${m_i}$, ${l_i}$）。

FlashAttention-2 forward pass. 如图所示，FlashAttention-2将 Q 移到了外循环 i，K V移到了内循环 j，并将 Q 分为4个warp，所有warp都可以访问 K 和 V。这样做的好处是，原来 FlashAttention 每次内循环 i++ 会导致 ${O_i}$ 也变换（而 ${O_i}$ 需要通过HBM读写），现在每次内循环 j++ 处理的都是 ${O_i}$，此时 ${O_i}$ 是存储在SRAM上的，代价远小于HBM。

3. flash attention V3

论文：Flash-Decoding for long-context inference

链接：https://crfm.stanford.edu/2023/10/12/flashdecoding.html

Flash-Decoding借鉴了FlashAttention的优点，将并行化维度扩展到keys/values序列长度。这种方法几乎不受序列长度影响（这对LLM模型能力很重要），可以充分利用GPU，即使在batch size较小时（inference特点），也可以极大提高了encoding速度。

3.1 Motivation

最近，像ChatGPT或Llama这样的LLM模型受到了空前的关注。然而，它们的运行成本却非常高昂。虽然单次回复的成本约为0.01美元（例如在AWS 8块A100上运行几秒钟），但是当扩展到数十亿用户的多次交互时，成本会迅速上升。而且一些场景的成本更高，例如代码自动补全，因为只要用户输入一个新字符就会执行。由于LLM应用非常广泛且还在迅速增长，即使稍微提升其运行效率也会产生巨大的收益。

LLM inference（或称为decoding）是一个迭代的过程：预测的tokens是逐个生成的。如果生成的句子有N个单词，那么模型需要进行N次forward。一个常用的优化技巧是KV Cache，该方法缓存了之前forward的一些中间结果，节约了大部分运算（如MatMul），但是attention操作是个例外。随着输出tokens长度增加，attention操作的复杂度也极具上升。

然而我们希望LLM能处理长上下文。增加了上下文长度，LLM可以输出更长的文档、跟踪更长的对话，甚至在编写代码之前处理整个代码库。例如，2022年大多数LLM的上下文长度最多为2k（如GPT-3），但现在LLM上下文长度可以扩展到32k（Llama-2-32k），甚至最近达到了100k（CodeLlama）。在这种情况下，attention操作在推理过程中占据了相当大的时间比例。此外，当batch size增加时，即使在相对较小的上下文中，attention操作也可能成为瓶颈。这是因为该操作需要对内存的访问会随着batch size增加而增加，而模型中其他操作只和模型大小相关。

因此，本文提出了Flash-Decoding，可以推理过程中显著加速attention操作（例如长序列生成速度提高8倍）。其主要思想是最大化并行加载keys和values的效率，通过重新缩放组合得到正确结果。

3.2 Multi-head attention for decoding

在decoding过程中，每个生成的新token需要与先前的tokens合并后，才能继续执行attention操作，即 ${softmax(Q \times K^T) \times V}$。Attention操作在训练过程的瓶颈主要卡在访问内存读写中间结果（例如 ${Q \times K^T}$）的带宽，相关加速方案可以参考FlashAttention V1和FlashAttention V2。

然而，上述优化不适合直接应用于推理过程。因为在训练过程中，FlashAttention对batch size和query length进行了并行化加速。而在推理过程中，query length通常为1，这意味着如果batch size小于GPU上的SM数量（例如A100上有108个SMs），那么整个计算过程只使用了GPU的一小部分！特别是当上下文较长时，通常会减小batch size来适应GPU内存。例如batch size = 1时，FlashAttention对GPU利用率小于1%！

从下图也可以看出，FlashAttention是按顺序更新output的，其实在看FlashAttention这篇文章时就觉得这个顺序操作可以优化的，因为反正都要rescale，不如最后统一rescale，没必要等之前block计算完（为了获取上一个block的max值）

3.3 A faster attention for decoding: Flash-Decoding

上面提到FlashAttention对batch size和query length进行了并行化加速，Flash-Decoding在此基础上增加了一个新的并行化维度：keys/values的序列长度。即使batch size很小，但只要上下文足够长，它就可以充分利用GPU。与FlashAttention类似，Flash-Decoding几乎不用额外存储大量数据到全局内存中，从而减少了内存开销。

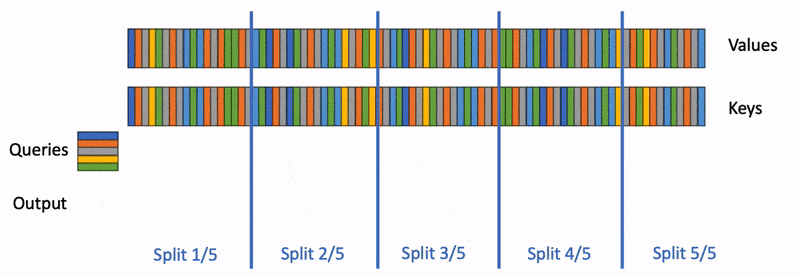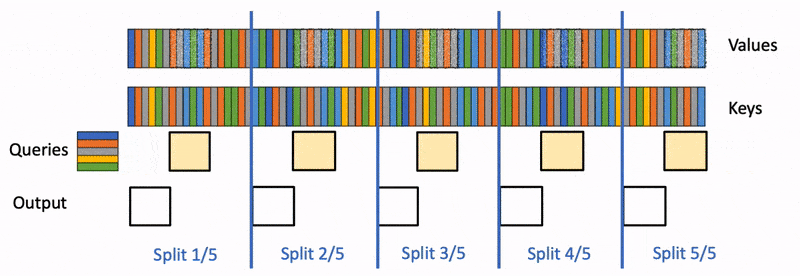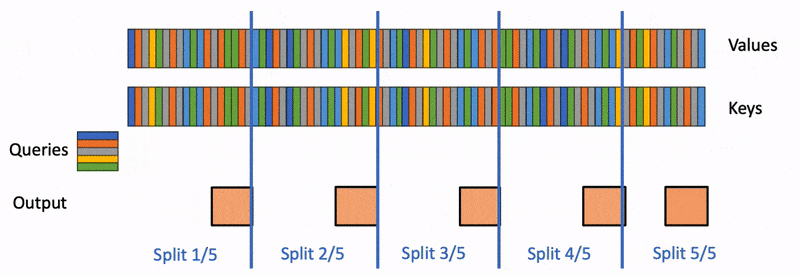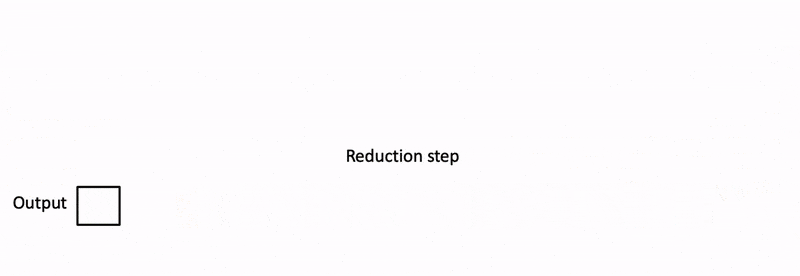
Flash Decoding主要包含以下三个步骤（可以结合上图来看）：

• 将keys和values分成较小的block
• 使用FlashAttention并行计算query与每个block的注意力（这是和FlashAttention最大的区别）。对于每个block的每行（因为一行是一个特征维度），Flash Decoding会额外记录attention values的log-sum-exp（标量值，用于第3步进行rescale）
• 对所有output blocks进行reduction得到最终的output，需要用log-sum-exp值来重新调整每个块的贡献

实际应用中，第1步中的数据分块不涉及GPU操作（因为不需要在物理上分开），只需要对第2步和第3步执行单独的kernels。虽然最终的reduction操作会引入一些额外的计算，但在总体上，Flash-Decoding通过增加并行化的方式取得了更高的效率。

Flash-Decoding对LLM在GPU上inference进行了显著加速（尤其是batch size较小时），并且在处理长序列时具有更好的可扩展性。

4. flash attention V4

论文：FlashDecoding++Faster Large Language Model Inference on GPUs

链接：https://arxiv.org/abs/2311.01282

4.1 Introdcution

为了提高softmax并行性，之前方法（FlashAttention、FlashDecoding）将计算过程拆分，各自计算partial softmax结果，最后需要通过同步操作来更新partial softmax结果。例如FlashAttention每次计算partial softmax结果都会更新之前的结果，而FlashDecoding是在最后统一更新所有partial softmax结果。

LLM推理加速面临的三大挑战：

• 在A100 GPU上分析了输入长度为1024的情况，这种同步partial softmax更新操作占Llama2-7B推理的注意力计算的18.8%。
• 在解码阶段，Flat GEMM操作的计算资源未得到充分利用。这是由于解码阶段是按顺序生成token（一次只生成一个token），GEMM操作趋于flat-shape，甚至batch size等1时变成了GEMV（General Matrix-Vector Multiplication），具体看论文Figure 2。当batch size较小时（e.g., 8），cublas和cutlass会将矩阵填充zeros以执行更大batchsize（e.g., 64）的GEMM，导致计算利用率不足50%。
• 动态输入和固定硬件配置影响了LLM推理的性能。例如，当batch size较小时，LLM推理的解码过程是memory-bounded，而当batch size较大时是compute-bounded。

针对这3个问题，本文分别提出了对应优化方法：

• Asynchronized softmax with unified max value. FlashDecoding++为分块softmax计算设置了一个共享的最大值。这样可以独立计算partial softmax，无需同步更新。
• Flat GEMM optimization with double buffering. FlashDecoding++只将矩阵大小填充到8，对比之前针对flat-shaped GEMM设计的为64，提高了计算利用率。论文指出，具有不同shape的flat GEMMs面临的瓶颈也不同，于是进一步利用双缓冲等技术提高kernel性能。
• Heuristic dataflow with hardware resource adaption. FlashDecoding++同时考虑了动态输入和硬件配置，针对LLM推理时数据流进行动态kernel优化。

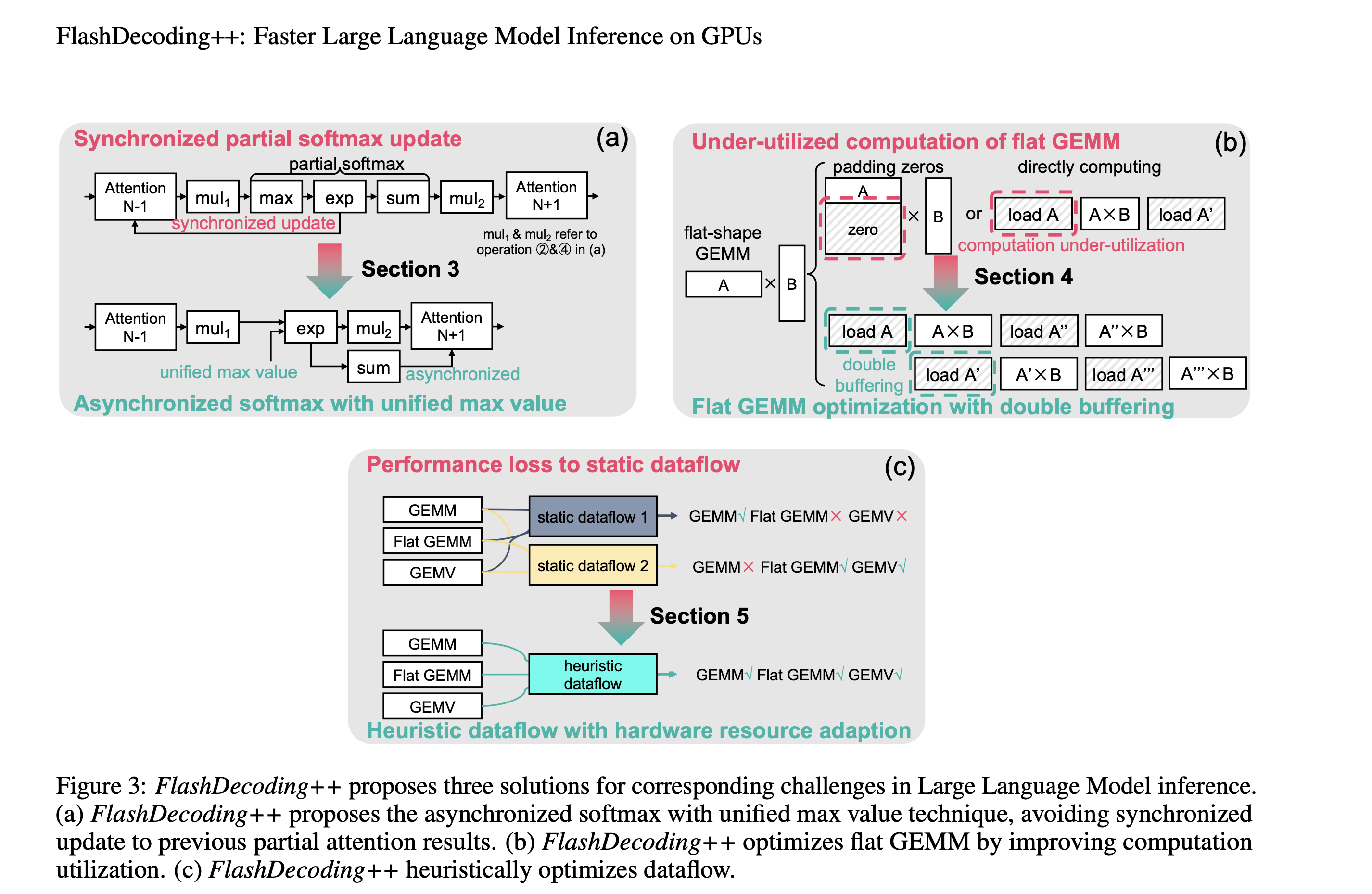
4.2 Backgrounds

LLM推理中的主要操作如下图所示：linear projection(①和⑤)、attention(②、③和④)和feedforward network(⑥)。为简单起见，这里忽略了position embedding、non-linear activation、mask等操作。

本文将LLM推理时对Prompt的处理过程称为prefill phase，第二阶段预测过程称为decode phase。这两个阶段的算子基本一致，主要是输入数据的shape是不同的。由于decode phase一次只处理一个令牌（batch size=1，或batch size很小），因此输入矩阵是flat-shape matrices（甚至是vectors），参见下图Decode phase部分中和KV Cache拼接的红色向量。

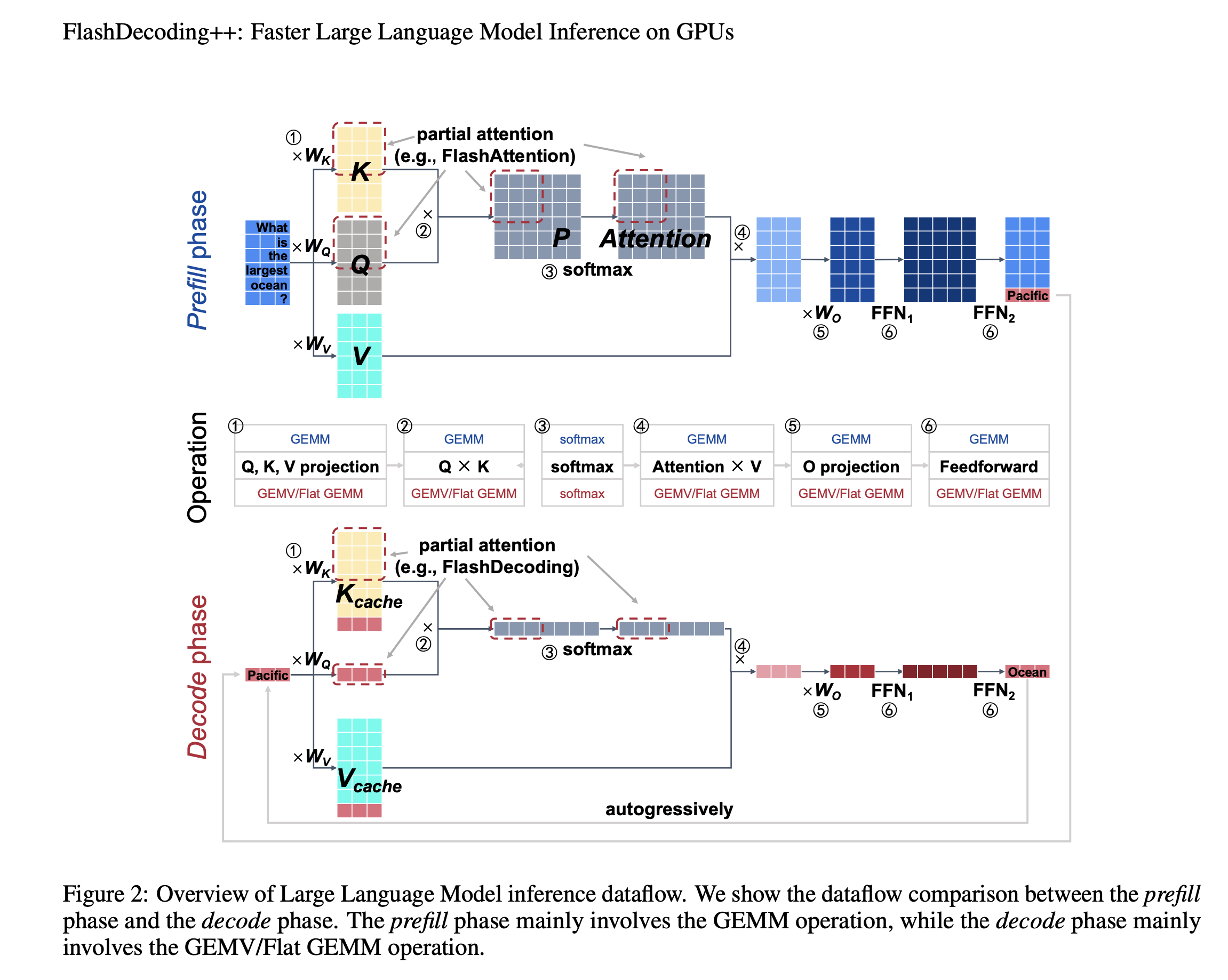
LLM推理中的另一个问题就是Softmax算子，其需要计算并存储所有全局数据，并且数据量随着数据长度成平方增长，存在内存消耗高和低并行性等问题。

4.3 Asynchronized Softmax with Unified Maximum Value

FlashAttention和FlashDecoding对softmax操作进行了分块处理，但是块与块之间需要进行同步（主要是局部最大值）。本文发现这种同步操作的开销约为20%。因此，作者希望去除同步操作，也就是独立计算出partial softmax结果。

其实方案就是找到一个合适的公共最大值 ${\phi}$。然而，如果 ${\phi}$ 太大，会造成 ${e^{x_i-\phi}}$ 溢出；如果 ${\phi}$ 太小，会造成精度损失。于是作者进行了统计，如下图所示。例如，对于Llama2-7B， >超过99.99%的值在[-16.8, 6.5]之间。

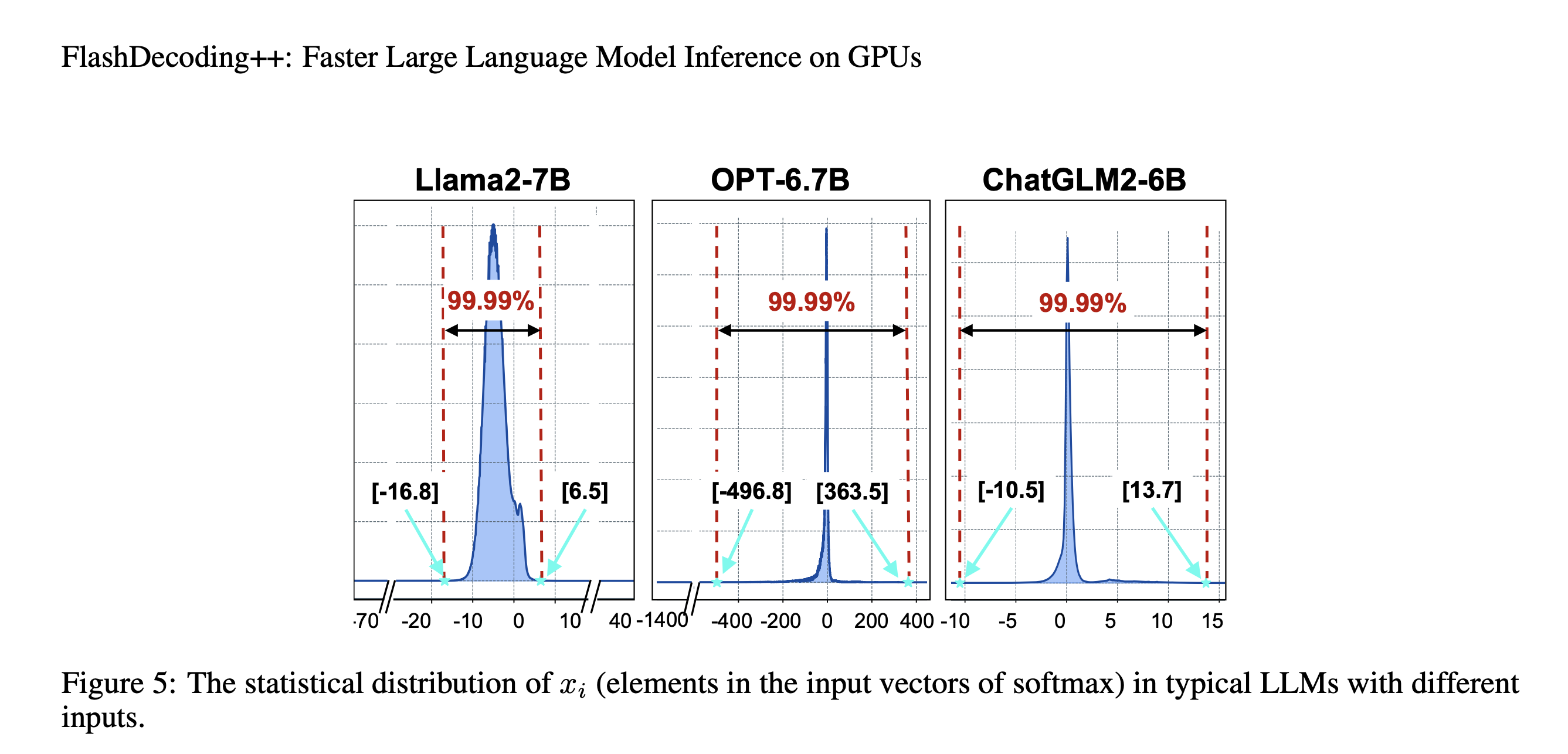
但是对于OPT-6.7B来说，其范围较大，于是作者采用动态调整策略，如果在推理过程中发现设置的 ${\phi}$ 不合理，那么就终止当前操作，然后采用FlashAttention和FlashDecoding的方法计算softmax。下图b中展示当 ${e^{9-6}}$ 超过阈值 ${e^3}$ 时的recompution过程。

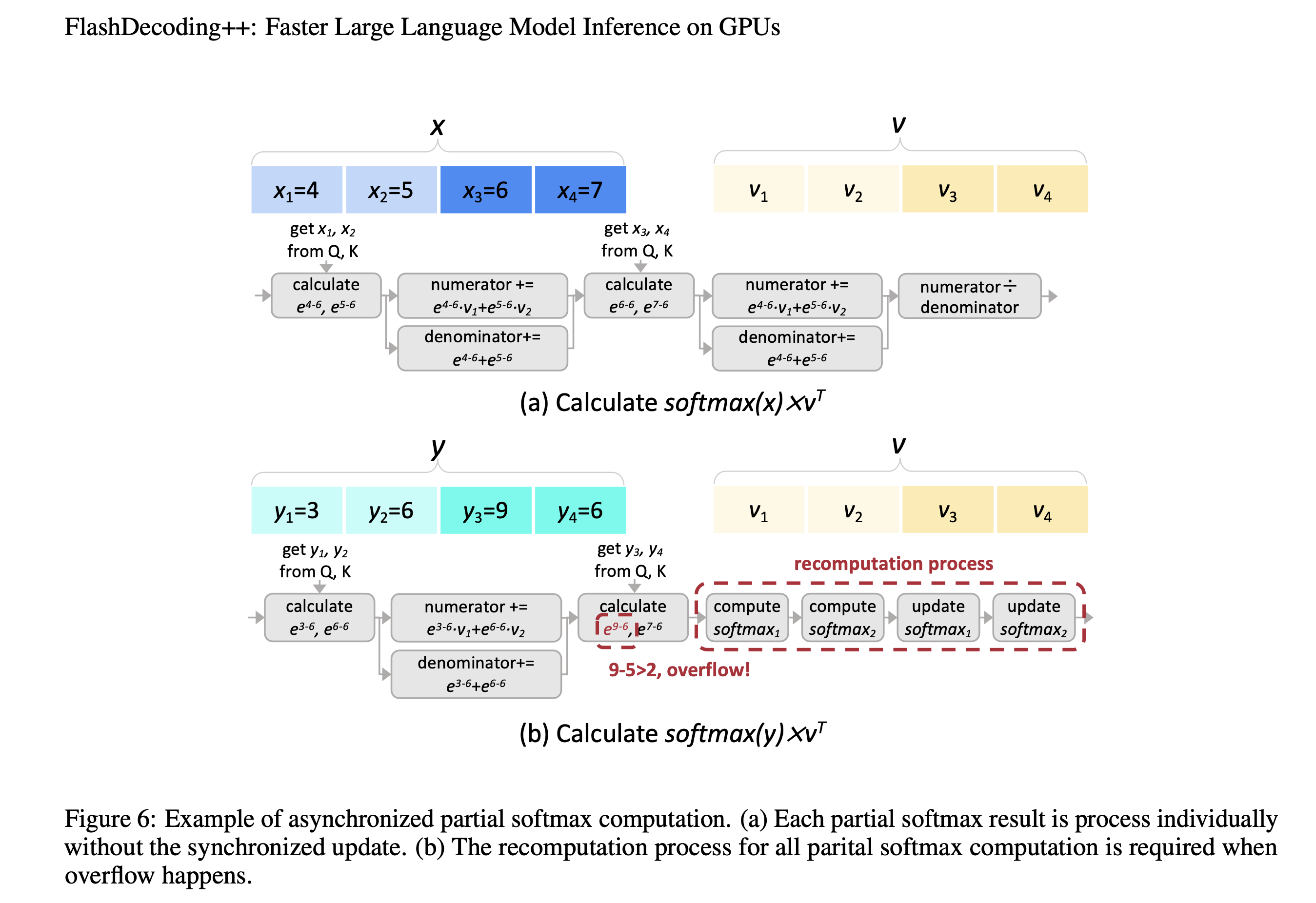
4.4 Flat GEMM Optimization with Double Buffering

Decoding阶段的过程主要由GEMV（batch size=1）或flat GEMM（batch size>1）。

GEMV/GEMM运算可以用 $M 、 N 、 K$ 来表示, 其中两个相乘矩阵的大小分别为 $M \times K$ 和 $K \times N$ 。一般 LLM推理引擎利用Tensor Core使用cuBLAS和CUTLASS等库来加速。尽管Tensor Core适合处理M $=8$ 的GEMM, 但这些库为了隐藏memory latency, 通常将M维度平铺到64。然而, decode phase的GEMV或flat GEMM的M通远小于64, 于是填充0到64, 导致计算利用率低下。

若假设 $N$ 维度上和 $K$ 维度上的tiling size分别为 $B_N$ 和 $B_K$, 那么每个GEMM tile的计算量为 $2 \times M \times B_N \times B_K$ （这里的2表示乘加2次）, 总共有 $B=\frac{N \times K}{B N \times B K}$ 个GEMM tiles。总内存访问量为 $\left(M \times B_K+B_N \times B_K\right) \times B+M \times N$ 。因此, 计算和内存比为:

另一方面, tiling后的并行度是 $N / B_N$ 。于是发现了GEMV或falt GEMM两者矛盾之处：计算和内存比与 $B_N$ 正相关, 而并行度与 $B_N$ 负相关。下图展示了 GEMM在不同 $B_N$ 和 $N$ 下的性能（归一化后)。本文总结了两个关键结论:

1. 当 $N$ 较小时, flat GEMM是parallelism-bounded。NVIDIA Tesla A100中有108个Streaming Multiprocessors (SMs), 于是应该将 $N / B_N$ 设置为一个相关的数 (128或256)。
2. 当 $N$ 较大时, flat GEMM是memory-bounded。通过隐藏memory access latency可以提高性能。

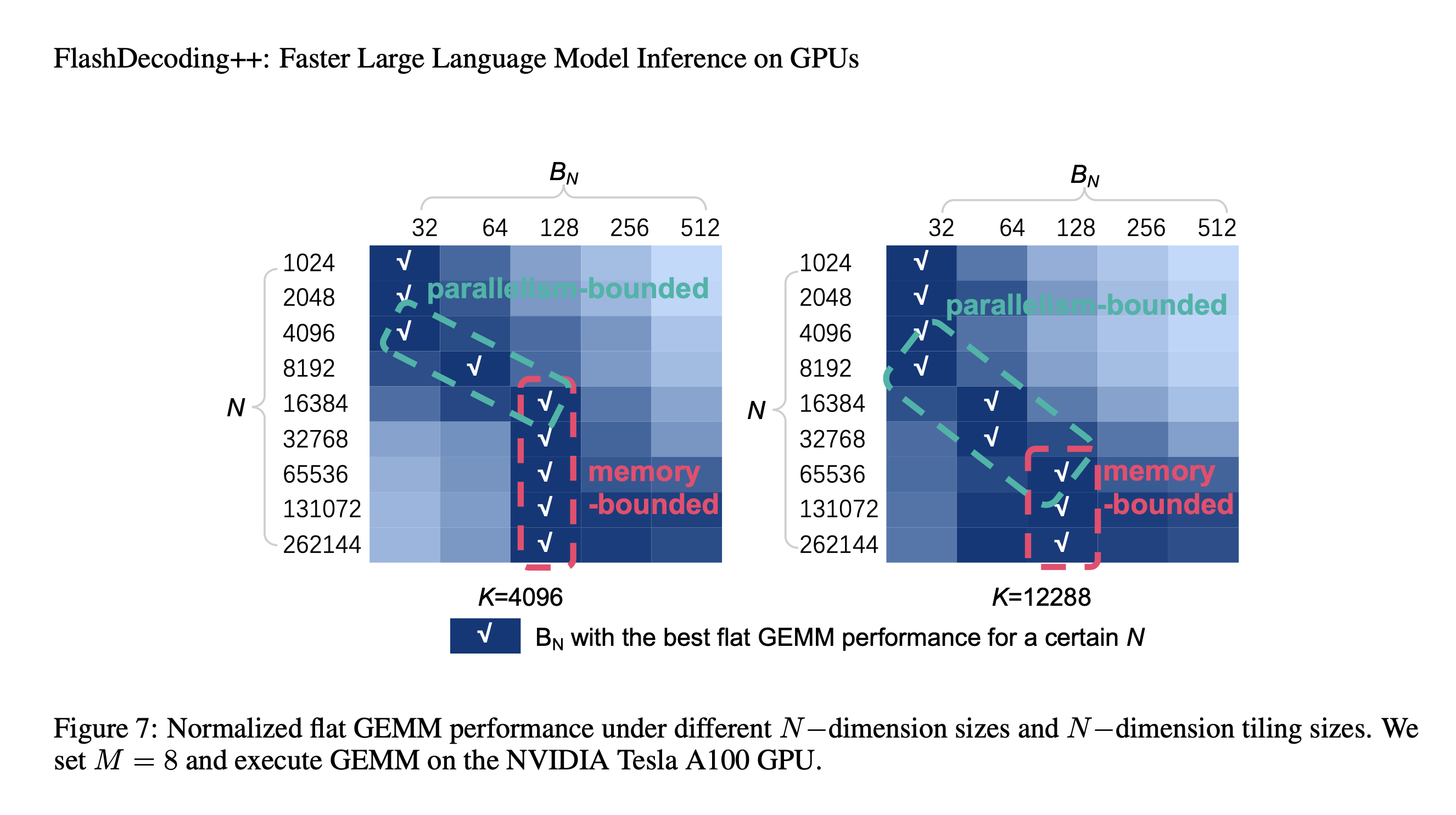
为了隐藏 memory access latency，本文引入了double buffering技术。具体来说就是在共享内存中分配两个buffer，一个buffer用于执行当前tile的GEMM计算，同时另一个buffer则加载下一个tile GEMM所需的数据。这样计算和内存访问是重叠的，本文在 $N$ 较大时采取这种策略，下图为示意图。

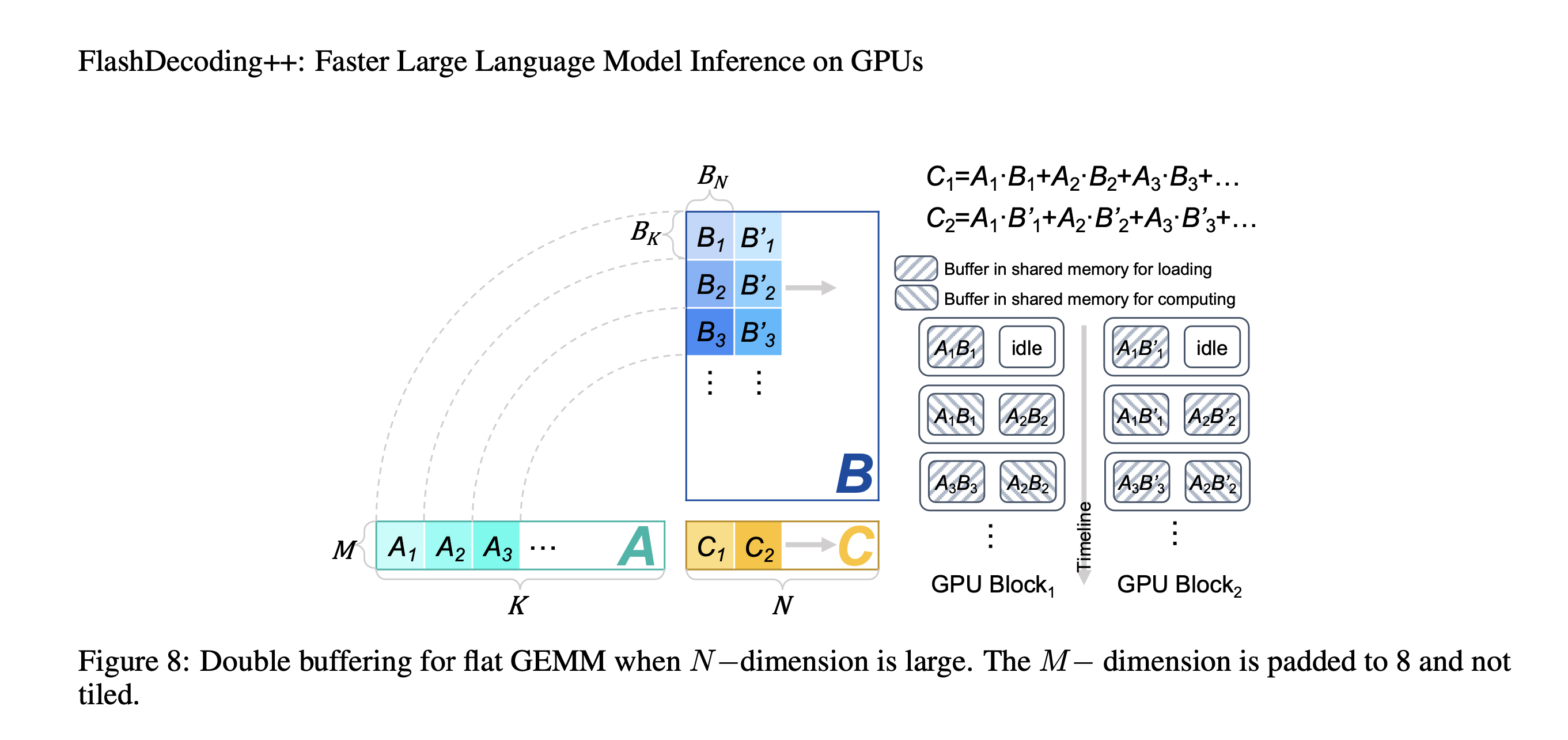
4.5 Heuristic Dataflow with Hardware Resource Adaption

影响LLM推理性能的因素有很多：（a）动态输入。batch size和输入序列长度的变化造成了工作负载变化。（b）模型多样性。主要指模型结构和模型大小。（c）GPU能力不同。例如内存带宽、缓存大小和计算能力。（d）工程优化。

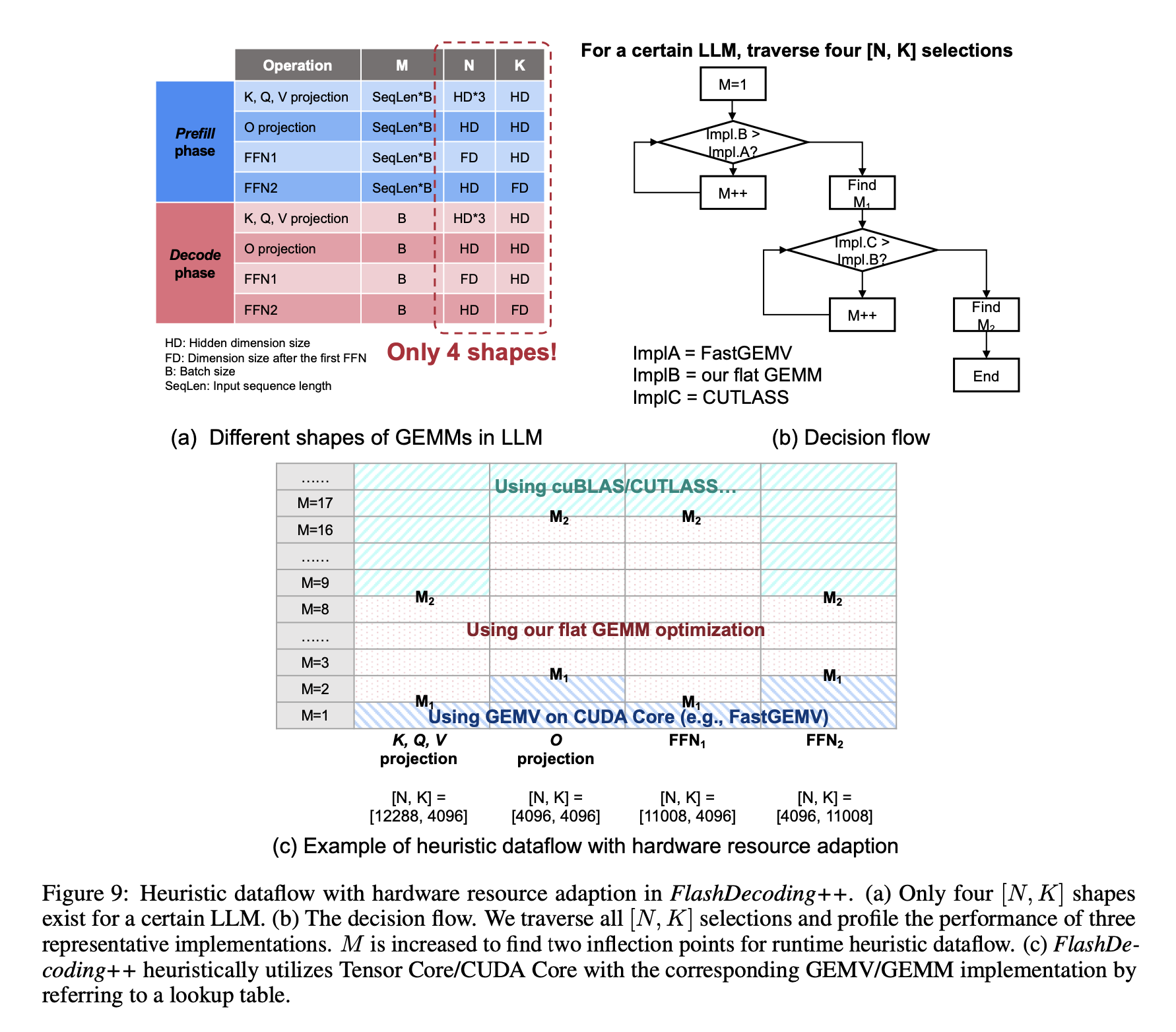
虽然这些因素构建了一个很大的搜索空间，但LLM中不同layer的同质性大大减少了算子优化的搜索空间。例如，prefill phase和decode phase中有4个GEMV/GEMM操作（K、Q、V投影、O投影、2个FFN），都可以表示为[M, K]和N x K，对应了四种[N, K]组合，如下图所示。此外，prefill phase的M与输入序列长度和batch size有关，decode phase的M只与batch size有关。

本文根据不同的 M, K, N 选取FastGEMV、flat GEMM（本文方法）、CUTLASS。